8.7.2 Анализ концентрированных данных

На предприятии с семнадцатью работниками девять из них удовлетворены условиями труда. Двое из этой последней группы в текущем году болели гриппом; из восьми работников, которые не удовлетворены условиями труда, гриппом болели пятеро. Это дает нам следующую таблицу:

удовлетворены

не уловлетворены

болели

не болели

Следует выяснить, является ли значимой большая доля болевших среди неудовлетворенных условиями труда. Подходящим статистическим тестом для этой задачи будет точный тест Фишера и Йейтса, который выполняется после создания таблицы сопряженности в дополнении к обычному тесту %2, если количество наблюдений очень мало.

Чтобы можно было решить эту задачу с применением SPSS, в первую очередь следует построить соответствующий файл данных, состоящий из наблюдений и переменных. Примером такого файла служит grippe.sav. Загрузите этот файл. В окне редактора данных вы получите структуру с четырьмя наблюдениями и тремя переменными.

Она содержит переменную grippe с категориями 1 и 2 (болели — не болели), переменную zuf с категориями 1 и 2 (удовлетворены — не удовлетворены) и переменную freq, которая указывает частоту каждого сочетания и будет использоваться в качестве переменной взвешивания.

Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения)
В диалоговом окне Weight Cases выберите опцию Weight cases by и перенесите переменную freq в поле Frequency variable.
Закройте диалоговое окно и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)
Перенесите переменную grippe в список переменных строк (Rows), переменную zuf— в список переменных столбцов (Columns), и в диалоге, открываемом кнопкой Statistics..., задайте проведение теста %2 (Chi-square).

В окне просмотра появится следующий результат:

Таблица сопряженности Болели? * Удовлетворены?

Count (Количество)
		Удовлетворены?	Total
		да нет
Болели?	Да	2	5	7
	Нет	7	3	10
Total		9	8	17

Chi-Square Tests

	Value	df	Asymp. Sig. (2-sided)	Exact Sig. (2-sided) (Точная значимость (двусторон-няя))	Exact Sig. (1-sided) (Точная значимость (односторон-няя))
Pearson Chi-Square (?² пo Пирсону)	2,837 "	1	,092
Continuity Correction (b) (Коррекция непреры-вности)	1,418	1	,234
Likelihood Ratio (Отношение правдопо-добия)	2,915	1	,088
Fisher's Exact Test (Точный тест Фишера)				,153	,117
Linear-by-Linear Association (Зависимость линейный-линейный)	2,670	1	,102
N of Valid Cases (Кол-во допустимых случаев)	17

a. Computed only for a 2x2 table (Вычислено только для таблицы 2Х2)

b. 3 cells (75,0%) have expected count less than 5. The minimum expected count is 3,29 (3 ячейки (75%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)

Односторонний тест Фишера-Йейтса даст в этом случае р =0,117, т.е. отсутствие значимой разницы.

Следующий пример взят из биологии. Исследовалось количество особей девяти различных видов кузнечиков на пяти разных лугах. Частоты сведены в следующую таблицу

Луг

Вид кузнечика 1	2	3	4	5
1	0	0	1	1	1
2	1	1	1	1	0
3	61	51	17	122	54
4	36	32	23	38	11
5	2	0	2	6	0
6	3	1	2	2	1
7	0	0	0	2	0
8	26	50	25	54	22
9	35	33	36	25	12

Следует выяснить, являются ли повышенная концентрация или недостаток отдельных видов кузнечиков на определенных лугах статистически значимыми. Для этого следует применить тест по критерию хи-квадрат.

И в этом случае решение задачи SPSS должна начаться с составления файла данных, содержащего три переменные: переменную для вида кузнечиков (с категориями 1—9), переменную для луга (категории 1—5) и переменную, содержащую частоту данного вида на данном лугу.

Загрузите файл wiese.sav и исследуйте его структуру в редакторе данных.
Выберите в меню команды Data (Данные) Weight Cases... (Взвесить наблюдения) Откроется диалоговое окно Weight Cases.
Выберите опцию Weight cases by и перенесите переменную h в поле Frequency variable.
Закройте диалоговое окно кнопкой ОК и выберите команды меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

Появится диалоговое окно Crosstabs.

Перенесите переменную heuschr в список переменных строк, переменную wiese — в список переменных столбцов, и в диалоге, открываемом кнопкой Cells..., кроме вывода наблюдаемых частот (флажок Observed в группе Counts), задайте также вывод ожидаемых частот (флажок Expected) и нормированных остатков (флажок Standardized в группе Residuals). После закрытия диалогового окна будет выведена следующая таблица.

Таблица сопряженности HFUSflHR * WIFSF

	WIESE	Total
1	2	3	4	5
HEUSCHR
1	Count (Количество)	0	0	1	1	1	3
Expected Count (Ожидаемое количество)	,6	,6	,4	1,0	,4	3,0
Std. Residual (Нормиро- ванный остаток)	-,8	-,8	,9	,0	1,0
2	Count	1	1	1	1	0	4
Expected Count	,8	,8	,5	1,3	,5	4,0
Std. Residual	,2	,2	,6	-,2	-,7
3	Count	61	51	17	122	54	305
Expected Count	63,2	64,8	41,3	96,8	38,9	305,0
Std. Residual	-,3	-1,7	-3,8	2,6	2,4
4	Count	36	32	23	38	11	140
Expected Count	29,0	29,7	18,9	44,4	17,9	140,0
Std. Residual	1,3	,4	,9	-1,0	-1,6
5	Count	2	0	2	6	0	10
Expected Count	2,1	2,1	1,4	3,2	1,3	10,0
Std. Residual	-,1	-1,5	,6	1,6	-1,1
6	Count	3	1	2	2	1	9
Expected Count	1,9	1,9	1,2	2,9	1,1	9,0
Std. Residual	,8	-,7	,7	-,5	-,1
7	Count	0	0	0	2	0	2
Expected Count	,4	,4	,3	,6	,3	2,0
Std. Residual	-,6	-,7	-,5	1,7	-,5
8	Count	26	50	25	54	22	177
Expected Count	36,7	37,6	23,9	56,2	22,6	177,0
Std. Residual	-1,8	2,0	,2	-,3	-,1
9	Count	35	33	36	25	12	141
Expected Count	29,2	29,9	19,1	44,7	18,0	141,0
Std. Residual	1,1	,6	3,9	-3,0	-1,4
Total
Count	164	168	107	251	101	791
Expected Count	164,0	168,0	107.0	251,0	101,0	791,0

В ячейках таблицы последовательно располагаются наблюдаемые частоты (fy), ожидаемые частоты (fg) и нормированные остатки, определяемые по формуле:

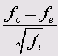
Нормированный остаток	Уровень значимости
>=2,0	р<0,05 (*)
>=2,6	р<0,01 (**)
>=3,3	P<0,001 (***)

Однако эти правила применимы, только в том случае, если ожидаемая частота не меньше 5. Если, к примеру, взять вид кузнечиков № 3, то для него наблюдается значимый недостаток на лугу 3, очень значимая концентрация на лугу 4 и значимая концентрация на лугу 5.

Содержание раздела