Задачи статистики в пакете SPSS
         

8.7.1 Коррекция при отсутствии репрезентативности

Перед служащими и представителями других социальных групп были поставлены четыре классических вопроса Инглхарта, уже известные нам из раздела 8.4.2, то есть, было предложено выбрать одну из четырех степеней важности для каждого из нижеследующих пунктов:

1. Поддержание спокойствия и порядка

2. Усиление влияния граждан на власть

3. Борьба с инфляцией

4. Обеспечение свободного выражения мнений

Данные, взятые из опроса ALLBUS 1988 г., хранятся в файле beamte.sav. При этом переменной beamier присваивается кодировка 1 или 2 в зависимости от того, является ли респондент служащим; переменные themal-Hhema4 содержат оценки четырех вышеприведенных пунктов.



  •  Загрузите файл beamte.sav и командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных beamier и themaS:

Служащий?

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

Да

137

10,5

10,5

10,5

Нет

1162

89,5

89,5

100,0

Total

1299

100,0

100,0

Борьба с инфляцией

Valid

первостепенная важность

Frequency 109

Percent 8,4

Valid Percent 8,4

Cumulative Percent 8,4

второстепенная важность

237

18,2

18,2

26,6

важность третьей степени

374

28,8

28,8

55,4

важность четвертой степени

579

44,6

44,6

100,0

Total

1299

100,0

100,0

Из частотной таблицы переменной beamier можно заключить, что в данной выборке 10,5% респондентов являются служащими, хотя известно, что доля служащих в общем населении составляет только 8,4%.

Прежде чем мы скорректируем это небольшое искажение при помощи переменной взвешивания, составим таблицу сопряженности для переменных themaS (строки) и beamter (столбцы).

  •  Командами меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности) создайте таблицу сопряженности из этих переменных.
  •  Дополнительно кнопкой Cells... (Ячейки) задайте вывод процентов по строкам (Percentages — Row) и столбцам (Column), а кнопкой Statistics... (Статистика) — выполнение теста %2(Chi-square):

Таблица сопряженности Борьба с инфляцией* Служащий?

Служащий?
Да

нет

Total

Борьба с инфля- цией

первостепен ная важность

Count (Коли- чество)

6

103

109

% от Борьба с инфляцией

5,5%

94,5%

100,0%

%от Служащий?

4,4%

8,9%

8,4%

второстепенн ая важность

Count

14

223

237

% от Борьба с инфляцией

5,9%

94,1%

100,0%

%от Служащий?

10,2%

19,2%

18,2%

важность третьей степени

Count

37

337

374

% от Борьба с инфляцией

9,9%

90,1%

100,0%

%от Служащий?

27,0%

29,0%

28,8%

важность четвертой степени

Count

80

499

579

% от Борьба с инфляцией

13,8%

86,2%

100,0%

%от Служащий?

58,4%

42,9%

44,6%

Total

Count

137

1162

1299

% от Борьба с инфляцией

10,5%

89,5%

100,0%

%от Служащий?

100,0%

100,0%

100,0%

Chi-Square Tests (Тесты хи-квадрат)

Value (Значение)

df

Asymp. Sig. (2-sided) (Асимптотическая значимость (двусторонняя))

Pearson Chi-Square хи-квадрат по Пирсону)

15,077 (а)

3

,002

Likelihood Ratio (Степень правдоподобия)

16,032

3

,001

Linearly-Linear Association (Зависимость линейный-линейный)

14,302

1

,000

N of Valid Cases (Кол-во допустимых случаев)

1299

a. 0 cells (,0%) have expected count less than 5. The minimum expected count is 11,50. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 11,50.)

Результаты показывают, что для служащих борьба с инфляцией имеет меньшее значение, чем для остальных респондентов.

Теперь путем взвешивания мы попробуем скорректировать искажение доли служащих, имеющееся в выборке. Принцип заключается в том, что для каждого значения переменной (в данном случае переменной beamier) вычисляется весовой коэффициент как отношение необходимого значения к существующему.

 Весовой коэффициент = (необходимое значение)/(существующее значение)

Для служащих весовой коэффициент равен

8,4/10,5=0,8

 а для остальных —

91,5/89,5 = 1,023 

  •  Командами меню File (Файл) New (Создать) Syntax (Синтаксис) откройте редактор синтаксиса.
  •  Чтобы создать переменную взвешивания, введите следующие команды: 
IF beamter=1 gewicht=8.4/10.5 . 
 IF beamter=2 gewicht=91.6/89. 5 . 
  EXECUTE .
Исходя из соображений точности расчета рекомендуется вводить сами значения, а не их отношения, и предоставлять их вычисление компьютеру.

  •  Выделите введенные команды, выбрав в меню Edit (Правка) Select All (Выделить все)
  •  Щелкните на символе Run, и в файл данных будет добавлена новая переменная gewicht. Ее мы и будем использовать как переменную взвешивания.
Для создания переменных взвешивания можно и не использовать команды синтаксиса SPSS, а повторить подход, описанный в разделе 8.4.1.

  •  Выберите в меню команды Data (Данные) ; Weight Cases... (Взвесить наблюдения)
 Появится диалоговое окно Weight Cases.

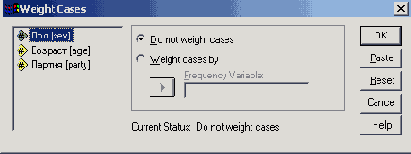
Рис. 8.13: Диалоговое окно Weight Cases

  •  Выберите в этом диалоговом окне опцию Weight cases by и перенесите переменную gewicht в поле под ней (в диалоге это поле называется Frequency Variable).
  •  Описанным выше путем создайте частотные таблицы переменных beamier и thema3 и таблицу сопряженности из этих переменных. Вы получите следующий результат:

Служащий?

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

да

110

8,4

8,4

8,4

нет

1189

91,6

61,6

100,0

Total

1299

100,0

100,0

Борьба с инфляцией

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

первостепенная важность

110

8,5

8,5

8,5

второстепенная важность

239

18,4

18,4

26,9

важность третьей степени

375

28,8

28,8

55,8

важность четвертой степени

575

44,2

44,2 ,

100,0

Total

1299

100,0

100,0

Таблица сопряженности Борьба с инфляцией * Служащий?

Служащий?
да

Нет

Total

Борьба с инфляцией

 первосте- пенная важность

 Count

5

105

110

% от Борьба с инфляцией

4,5%

95,5%

100,0%

%от Служащий?

4,5%

8,8%

8,5%

второсте- пенная важность

 Count

11

228

239

% от Борьба с инфляцией

4,6%

95,4%

100,0%

%от Служащий?

10,0%

19,2%

18,4%

важность третьей степени

 Count

30

345

375

% от Борьба с инфляцией

,U /0

92,0%

100,0%

%от Служащий?

27,3%

29,0%

28,9%

важность четвертой степени

 Count

64

511

575

% от Борьба с инфляцией

11,1%

88,9%

100,0%

%от Служащий?

58,2%

43,0%

44,3%

Total

Count

110

1189

1299

% от Борьба с инфляцией

8,5%

91,5%

100,0%

%от Служащий?

100,0%

100,0%

100,0%

Chi-Square Tests

Value

Df

Asymp. Sig. (2-sided)

Pearson Chi-Square

12,156 a

3

,007

Likelihood Ratio

12,972

3

,005

Linear-by-Linear Association

11,410

1

,001

N of Valid Cases

1299

а. 0 cells (,0%) have expected count less than 5. The minimum expected count is 9,31. (Ячейки с нулями (,0%) имеют ожидаемую частоту менее 5. Минимальная ожидаемая частота 9,31.)

Общая частота осталась неизменной — 1299, но взаимное отношение частот изменилось. В переменной beamter количество служащих снизилось с 137 до 110, что соответствует реальной доле служащих 8,4%. Также незначительно изменилась частотная таблица для переменной themaS; взвешивание повлияло и на нее.

То же можно сказать и о таблице сопряженности. Однако здесь процентные значения по столбцам не изменились; сохранились соотношения между отдельными значениями переменных в ячейках.

Установленное взвешивание будет действовать до тех пор, пока вы снова не выберете в диалоговом окне Weight Cases опцию Do not weight cases (He взвешивать наблюдения).

Описанный метод взвешивания при отсутствии репрезентативности может привести к возникновению некоторых проблем, которые, впрочем, не проявляются в изученном примере.

Если мы рассмотрим, например, взвешенную частотную таблицу переменной «Борьба с инфляцией», то обнаружим, что общее количество наблюдений (1299) не меняется при взвешивании. Это связано с тем, что сумма весовых коэффициентов по всем случаям равна числу случаев. Однако в варианте взвешивания, который будет изложен в разделе 8.7.2, это не так.

Если вы попробуете вручную просуммировать частоты упоминания всех четырех вариантов ответов, то в результате вы также получите число 1299. Однако это не закономерность, а скорее счастливое совпадение, о чем свидетельствует следующий пример.

  •  Загрузите файл mai.sav, содержащий результаты опроса членов профсоюза на тему 1 мая (см. главу 24).
  •  С помощью команд меню Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Frequencies... (Частоты) создайте частотные таблицы переменных v2 (Пол) и v20 (Занятие).

Пол

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

женский

77

28,4

28,4

28,4

мужской

184

71,6

71,6

100,0

Total

271

100,0

100,0

Занятие

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

Учащийся

8

3,0

3,0

3,0

Рабочий

47

17,3

17,3

20,3

Квалифици- рованный рабочий

47

17,3

17,3

37,6

Специалист

4

1,5

1,5

39,1

Служащий

66

24,4

24,4

63,5

Менеджер

8

3,0

3,0

66,4

Государствен- ный служащий

31

11,4

11,4

77,9

Пенсионер

42

15,5

15,5

93,4

Домохозяйка

g

3,3

3,3

96,7

Нетрудоспо- собный

1

,4

,4

97,0

Безработный Total

8 271

3,0 100,0

3,0 100,0

100,0

  •  Взвесим наблюдения так, чтобы устранить неравномерность между количествами респондентов обоих полов. Учитывая частотное распределение полов, характерное для имеющейся выборки, это выполняется при помощи следующих команд:
IF v2=1 w=135.5/77. 

IF v2=2 w=135.5/194.

 EXECUTE

  •  Теперь описанным выше способом проведем взвешивание, используя только что полученную переменную w, и построим обе частотные таблицы заново:

Пол

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

женский

135

50,0

50,0

50,0

мужской

135

50,0

50,0

100,0

Total

271

100,0

100,0

Занятие

Frequency

Percent

Valid Percent

Cumulative Percent

Valid

Учащийся

10

3,6

3,6

3,6

Рабочий

46

16,8

16,8

20,4

Квалифици- рованный рабочий

35

12,9

12,9

33,3

Специалист

3

1,0

1,0

34,4

Служащий

83

30,7

30,7

65,1

Менеджер

7

2,5

2,5

67,5

Государствен- ный служащий

32

11,9

11,9

79,4

Пенсионер

36

13,2

13,2

92,6

Домохозяйка

9

3,5

3,5

96,1

Нетрудоспо- собный

2

,6

,6

96,8

Безработный

9

3,2

3,2

100,0

Total

271

100,0

100,0

Хотя общее число наблюдений, 271, опять не изменилось, но суммирование частот по категориям дает несколько другие результаты.

Это особенно заметно для переменной Пол. Так как после определения переменной взвешивания обе категории должны иметь одинаковые частоты, с самого начала ясно, что сумма не может быть нечетной. Для переменной занятие сложение частот по категориям также дает результат 272, что на единицу отличается от общего количества наблюдений — 271, выводимого в окне просмотра. SPSS всегда, в том числе при взвешивании, выдает целочисленные частоты. Поэтому негативное влияние округления будет неизбежным. Другие статистические программы, например, Stata, обходят эту ситуацию, вычисляя взвешенные частоты с дробной частью.

Если сделать выборку наблюдений, то отображаемые программой суммы до и после взвешивания, как правило, также будут различаться. Это связано с тем, что в частичной выборке количество наблюдений обычно не соответствует сумме весовых коэффициентов, попадающих в эту выборку. Это можно проверить, создав на основе открытого файла данных частотную таблицу переменной «Занятие» до взвешивания и после взвешивания, но только для приверженцев партии СДПГ (v22=2). Тогда мы получим соответственно суммы 91 и 83.

Взвешивание для выравнивания характеристик при нарушении репрезентативности применяется в первую очередь при эпидемиологических исследованиях. Так как при весовом коэффициенте, превосходящем единицу, количество наблюдений искусственно увеличивается по сравнению с фактически измеренным, к результатам теста на значимость следует подходить весьма критически.

Содержание раздела