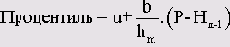6.3 Медиана для концентрированных данных
Для данных, имеющих форму частотной таблицы, определение медианы и остальных процентилей обычным методом будет слишком неточным. В таких случаях есть возможность вычислить медиану и любые другие процентили более точным методом. Мы поясним это на примере стоматологических данных.
-
Загрузите файл cpitn.sav, содержащий результаты стоматологического исследования.
Кроме переменных schule и mhfreq, которые определяют уровень образования и то, сколько раз в день обследуемый чистит зубы, этот файл содержит шесть переменных cpitnl—cpitn6, которые указывают степень пародонтального заболевания каждой из шести частей челюсти — так называемый параметр CPITN, задаваемый с помощью следующей кодировочной таблицы:
|
0
|
Здоровый пародонт
|
|
1
|
Кровоточивость
|
|
2
|
Зубные отложения
|
|
3
|
Глубина десенных карманов 3,5-5,5 мм
|
|
4
|
Глубина десенных карманов 6 мм и более
|
-
С помощью команд меню Analyze (Анализ)
Descriptive Statistics (Дескриптивные статистики) Frequencies (Частоты)
создайте частотную таблицу, к примеру, для переменной cpitnl. Если задать вычисление среднего значения и медианы, мы получим следующий результат:
Статистика
|
CPITN1
|
|
N
|
Допустимые
|
2548
|
|
|
Утерянные
|
0
|
|
Среднее значение
|
|
2,24
|
|
Медиана
|
|
2,00
|
CPITN1
|
|
Частота
|
Проценты
|
допустимые проценты
|
накопленные проценты
|
|
Допустимые здоровый
|
109
|
4,3
|
4,3
|
4,3
|
|
кровоточивость
|
389
|
15,3
|
15,3
|
19,5
|
|
отложения
|
921
|
36,1
|
36,1
|
55,7
|
|
глубина карманов
|
1042
|
40,9
|
40,9
|
96,6
|
|
3,5-5,5 глубина карманов >=6
|
87
|
3,4
|
3,4
|
100,0
|
|
Всего
|
2548
|
100,0
|
100,0
|
|
При определении медианы обычным методом ее значение равно 2. Это значение, хотя формально и правильное, но дает совершенно неудовлетворительный, недостаточно значимый результат. В данном случае, когда данные являются концентрированным, для уточнения медианы применяется следующая расчетная формула:
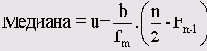
|
n
|
Количество измеренных значений
|
|
m
|
Класс, в котором находится медиана
|
|
u
|
Нижняя граница класса m
|
|
fm
|
Абсолютная частота в классе m
|
|
Fm-1
|
Накопленная частота вплоть до предыдущего класса
m — 1
|
|
B
|
Ширина класса
|
Следовательно, решающее значение имеет правильный выбор границ классов; их следует выбирать так, чтобы значения кодовых чисел соответствовали середине каждого класса. В данном примере для границ классов следует выбрать значения
-0,5 0,5 1,5 2,5 3,5 4,5
Ширина класса равна 1.
Следовательно,
n = 2548
m = 3 (так как медиана находится в третьем классе)
u = 1,5
f
m = 921
F
m-1 = 109 + 389 = 498
b = 1
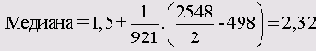
Описанный точный метод вычисления медианы будет использован в SPSS, если в диалоге Frequencies: Statistics установить флажок Values are group midpoints.
В этом случае мы получим точное значение медианы (2,32).
По определению, медиана — это значение, выше и ниже (правее и левее) которого расположено по 50 % всех значений, если они упорядочены по величине. Обобщая эту характеристику, мы приходим к определению так называемых процентилей. Эти характеристики позволяют, например, указать значение, ниже которого лежит 10 % всех значений (а выше расположено 90 % значений). Чаше всего применяются процентили 25 % и 75 %, называемые также соответственно первым и третьим квартилями.
В диалоге Frequencies: Statistics можно последовательно задать любые значения процентилей. Если данные концентрированы, снова следует установить флажок Values are group midpoints.
Формула вычисления процентиля для любого значения:
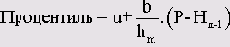
|
n
|
Класс, в котором находится процентиль
|
|
m
|
Нижняя граница класса т
|
|
P
|
Процентное значение процентиля
|
|
Нm
|
Процентная частота в классе m-1
|
|
Hm-1
|
Процентная накопленная частота в классе m-1
|
|
b
|
Ширина класса
|
Для процентиля 50 % (Р = 50) после некоторых преобразований получается формула для медианы, приведенная выше.
В столбчатых, линейных, круговых диаграммах и диаграммах с областями, на которых предусмотрено отображение медианы и других процентилей, при наличии концентрированных данных используется модифицированный способ расчета (см. раздел 22.1.1).
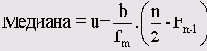
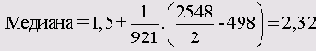 Описанный точный метод вычисления медианы будет использован в SPSS, если в диалоге Frequencies: Statistics установить флажок Values are group midpoints.
В этом случае мы получим точное значение медианы (2,32).
По определению, медиана — это значение, выше и ниже (правее и левее) которого расположено по 50 % всех значений, если они упорядочены по величине. Обобщая эту характеристику, мы приходим к определению так называемых процентилей. Эти характеристики позволяют, например, указать значение, ниже которого лежит 10 % всех значений (а выше расположено 90 % значений). Чаше всего применяются процентили 25 % и 75 %, называемые также соответственно первым и третьим квартилями.
В диалоге Frequencies: Statistics можно последовательно задать любые значения процентилей. Если данные концентрированы, снова следует установить флажок Values are group midpoints.
Формула вычисления процентиля для любого значения:
Описанный точный метод вычисления медианы будет использован в SPSS, если в диалоге Frequencies: Statistics установить флажок Values are group midpoints.
В этом случае мы получим точное значение медианы (2,32).
По определению, медиана — это значение, выше и ниже (правее и левее) которого расположено по 50 % всех значений, если они упорядочены по величине. Обобщая эту характеристику, мы приходим к определению так называемых процентилей. Эти характеристики позволяют, например, указать значение, ниже которого лежит 10 % всех значений (а выше расположено 90 % значений). Чаше всего применяются процентили 25 % и 75 %, называемые также соответственно первым и третьим квартилями.
В диалоге Frequencies: Statistics можно последовательно задать любые значения процентилей. Если данные концентрированы, снова следует установить флажок Values are group midpoints.
Формула вычисления процентиля для любого значения: