23.7 Гистограммы

Гистограммы отображают распределение переменных, принадлежащих к интервальной шкале. При таком отображении значения переменной разделяются на интервалы, производится подсчёт частот попадания отдельных значений переменных в эти интервалы и после этого полученные показатели представляются в форме столбцов, расположенных в непосредственной близости друг к другу. В соответствии с установками по умолчанию, количество и ширина интервалов выбирается программой автоматически; при желании эти величины могут быть установлены пользователем.

Отобразим при помощи гистограммы распределение показателей роста (переменная gr) группы пациентов из файла klin.sav.

Откройте файл klin.sav.
Выберите в меню Graphs (Графики) Interactive (Интерактивно) Histogram... (Гистограмма) Откроется диалоговое окно Create Histogram (Создание гистограммы).
Поместите переменную gr (рост) в поле оси х. В поле оси у оставьте системную переменную Scount (количество), устанавливаемую по умолчанию.
Откройте регистрационную карту Histogram (Гистограмма). Активируйте опцию Normal curve (Кривая нормального распределения). Оставьте автоматическую генерацию количества интервалов и ширины интервала.

Группирующую переменную Вы можете ввести в диаграмму посредством активирования оси г.

При помощи соответствующего выключателя активируйте ЗD-систему координат и в поле оси z перенесите переменную geschl (пол).

Рис. 23.45: Диалоговое окно Create Histogram (Создание гистограммы)

В трёхмерной системе координат мы уже видим две гистограммы. Отображение кривой нормального распределения в этом случае невозможно.

Вы можете организовать вывод так называемой кумулятивной гистограммы; интервальные частотные показатели при этом будут суммироваться.

Деактивируйте поле оси z и активируйте опцию Cumulative histogram (Кумулятивная гистограмма) (см. рис. 23.48).

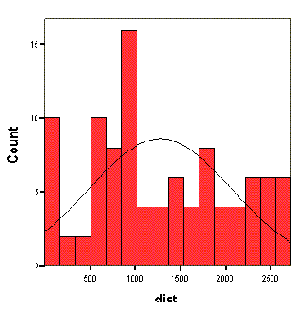
Рис. 23.46: Гистограмма с кривой нормального распределения

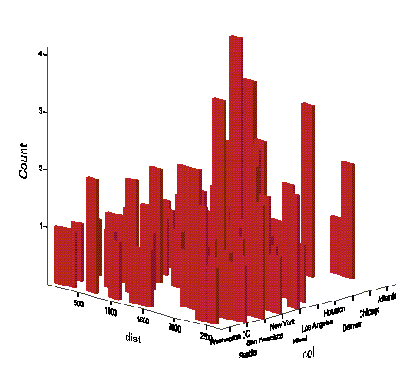
Рис.23.47: Группированная гистограмма

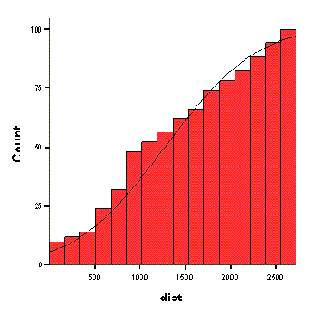
Рис. 23.48: Сводная гистограмма

Для того, чтобы решить, подчиняется ли рассматриваемая переменная нормальному распределению, недостаточно полагаться только на внешний вид гистограммы, а лучше провести более точный статистический тест. SPSS для этого предлагает тест Колмогорова-Смирнова (см. разд. 14.5); для нашего примера этот тест дает результат/> = 0,02, что говорит о значимом отклонении рассматриваемого распределения от нормального.

Содержание раздела