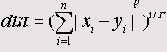Задачи статистики в пакете SPSS
20.3.1 Переменные, относящиеся к интервальной шкале (метрические переменные)
Для переменных такого рода на выбор предлагается восемь различных мер расстояния и мер сходства, которые мы и рассмотрим далее. Примером расчёта послужат два наблюдения из файла assess.sav (см. гл. 20.3), для которых расстояние и подобие должны быть рассчитаны с использованием переменных t3 и t4:| t3 | t4 | |
| Отто P. | 5 | 4 |
| Эльке М. | 4 | 10 |
Евклидова дистанция (расстояние)
Евклидова дистанция между двумя точками х и у — это наименьшее расстояние между ними. В двух- или трёхмерном случае — это прямая, соединяющая данные точки. Общей формулой для n-мерного случая (л переменных) является: 1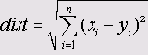
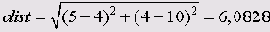
Квадрат евклидового расстояния
Этот вариант устанавливается по умолчанию. Благодаря возведению в квадрат при расчёте лучше учитываются большие разности. Эта мера должна всегда использоваться при построении кластеров при помощи центроидного и медианного методов, а также метода Варда (Ward-Method) (см. разд. 20.5).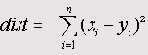
Косинус
Как и для корреляционных коэффициентов Пирсона, область значений этой меры находится между -1 и +1.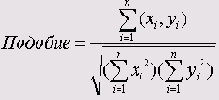
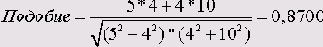
Корреляция Пирсона
Если кластеризация наблюдений осуществляется только на основании двух переменных, то корреляционный коэффициент Пирсона (см. разд. 15.1) со значениями находящимися в пределах от -1 до +1 не годится для использования в качестве меры подобия; он будет давать только значения -1 или +1.Чебышев (Chebychev)
Разностью двух наблюдений является абсолютное значение максимальной разности последовательных пар переменных, соответствующих этим наблюдениям. В приведенном примере абсолютная разность значений первой переменной равна 1, а второй переменной — 6. Поэтому разность Чебышева равна 6.Блок (Block)
Эта дистанционная мера, называемая также дистанцией Манхэттена или в шутку — дистанцией таксиста, определяется суммой абсолютных разностей пар значений. Для двумерного пространства это не прямолинейное евклидова расстояние между двумя точками, а путь, который должен преодолеть Манхэттенский таксист, чтобы проехать от одного дома к другому по улицам, пересекающимся под прямым углом.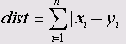
Минковский (Minkowski)
Расстояние Минковского равно корню r-ой степени из суммы абсолютных разностей пар значений взятых в r-ой степени: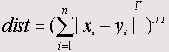
Пользовательская мера
Это обобщенный вариант расстояния Минковского. Это расстояние, называемое также степенным расстоянием, равно корню r-ой степени из суммы абсолютных разностей пар значений взятой в р-ой степени: