17.1.1 Одномерный дисперсионный анализ (общий многофакторный)

Исследуем влияние пола и возраста на результирующую величину показателя внимательности (M1). Здесь мы имеем дело с двумя факторами, из которых один (пол) разделён на две категории, а второй (возраст) на три. Комбинации этих двух факторов образуют в общей сложности шесть групп испытуемых (называемых также ячейками). Число наблюдений, относящихся к отдельным ячейкам является не одинаковым, а наоборот различным.

Откройте файл varana.sav.
Выберите в меню Analyze (Анализ) General Linear Model (Общая линейная модель) Univariate... (Одномерная) Откроется диалоговое окно Univariate (Одномерная) (см. рис. 17.2).
Перенесите переменную ml в поле зависимых переменных, а переменные geschl (пол) и alter (возраст) в поле фиксированных факторов.

Понятия "фиксированные" и "случайные" факторы требуют дополнительного объяснения. Фиксированными факторами или факторами с фиксированными эффектами называются такие факторы, которые охватывают все возможные классификационные слои одной независимой переменной, к примеру, пол мужской — женский или образование начальное — среднее — высшее. Однако, если слои (подпопуляции) фактора выбирается случайным образом из бесконечного множества возможных подпопуляции факторов, называемого генеральной популяцией, то говорят о факторах со случайными эффектами. В этом случае является уместным компонентный анализ, то есть расчёт так называемых компонентов дисперсии (см. гл. 17.4).

Щёлкните по кнопке Model... (Модель)

Откроется диалоговое окно Univariate: Model (Одномерная: Модель) (см. рис. 17.3).

Рис. 17.2: Диалоговое окно Univariate (Одномерная)

Рис. 17.3: Диалоговое окно Univariate: Model (Одномерная: Модель)

Модель дисперсионного анализа — это математическое соотношение, в котором каждая переменная представлена в виде суммы среднего значения и ошибки. Что касается выбора конкретной формы модели, то по умолчанию установлена полнофакторная модель Full factorial). В этой модели среднее значение каждого наблюдения представлено в виде генерального среднего и суммы вклада всех главных "эффектов" (факторов влияния), помимо которых производится также расчёт всех взаимодействий между факторами. Альтернативой является возможность выбора отдельных взаимодействий факторов влияния, которая осуществляется посредством активирования опции Custom (Пользовательский режим). Таким же образом должны быть отобраны и взаимодействия с ковариациями.

Для формирования сумм квадратов для МНК существует четыре различных подхода (четыре типа, обозначенных с помощью римских чисел I, II, III и IV), по умолчанию установлен тип III.

Оставьте в этом окне все установки по умолчанию и покиньте диалоговое окно нажатием кнопки Continue (Далее).
Щёлкните на выключателе Options... (Опции)

Откроется диалоговое окно Univariate: Options (Одномерная: Опции) (см. рис. 17.4)

Перенесите OVERALL (В целом) и обе переменные geschl (пол) и alter (возраст) в поле Display means for (Показать средние значения для); в этом случае в качестве результатов будут выведены средние значения и стандартная ошибка для совокупной выборки (OVERALL) и для всех слоев по обоим факторам. Средние значения для комбинаций взаимодействия на этом этапе рассчитываются только для неполнофакторных моделей.
Затем активируйте Descriptive Statistics (Дескриптивные статистики); благодаря выбору этой опции выводятся среднее значение, стандартные отклонения и количество наблюдений во всех ячейках.
Активируйте затем опцию Homogeneity tests (Тесты на однородность). Таким образом активируется проверка однородности дисперсии. Покиньте диалоговое окно нажатием Continue (Далее).
При помощи выключателя Plots... (Диаграммы) откройте диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы) (см. рис. 17.5).

Рис. 17.4: Диалоговое окно Univariate: Options (Одномерная: Опции)

Рис. 17.5: Диалоговое окно Univariate: Profile Plots (Одномерная: Профильные диаграммы)

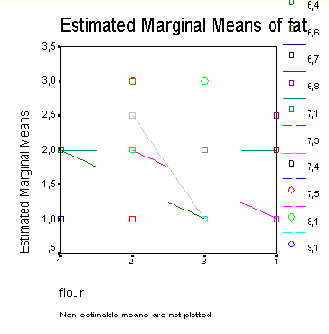
В случае профильных диаграмм речь идёт о графическом представлении средних значений слоев выбранных факторов в виде линейчатых диаграмм. При этом слои второго фактора соответственно могут быть использованы для отображения второй линии. Таким образом можно наглядно изобразить взаимодействия между двумя факторами.

Поместите переменную alter (возраст) в поле Horizontal Axis (Горизонтальная ось), а переменную geschl (пол) в поле Separate Lines (Отдельные линии). В принципе можно указывать дополнительную переменную и в поле Separate Plots (Отдельные графики); тогда для отдельных слоев этой переменной будут построены отдельные диаграммы.
Щёлкните на выключателе Add (Добавить) и покиньте диалоговое окно нажатием Continue (Далее).
В заключение щёлкните на выключателе Post Hoc... (Дополнительный тест). Откроется диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — множественные сравнения для наблюдаемых средних значений).

У Вас появится возможность выбрать один или несколько из восемнадцати тестов, необходимых для проведения дополнительного сравнения отдельных слоев выбранных факторов. Конечно же, это имеет смысл только для факторов с более чем двумя слоями.

Поместите переменную alter (возраст) в поле Post Hoc Tests for (Дополнительные тесты для).
Активируйте тест Шеффе (Scheffe). Теперь диалоговое окно выглядит так, как изображено на рисунке 17.6.
Покиньте диалоговое окно нажатием Continue (Далее).
Далее Вы имеете возможность определить контрасты и для каждого наблюдения сохранить некоторые статистические характеристики, как новые переменные. Мы от этого откажемся. Начните расчёт нажатием ОК.

В окне сначала появляется сводная таблица, озаглавленная "Межсубъектные факторы". Затем следует вывод средних значений, стандартных отклонений и количества наблюдений для отдельных ячеек, а также результаты теста на однородность.

Рис. 17.6: Диалоговое окно Univariate: Post Hoc Multiple Comparisons for Observed Means (Одномерная: Дополнительно — многократные сравнения для наблюдаемых средних значений)

Between-Subjects Factors (Межсубъектные факторы)

		Value Label (Метка значения)	N
GESCHL (Пол)	1	maennlich (Мужской)	15
2	weiblich (Женский)	12
ALTER (Возраст)	1	bis 30 Jahre (До 30 лет)	7
2	31 - 50 Jahre (31 - 50 лет)	9
3	ueber 50 Jahre (Свыше 50 лет)	11

Descriptive Statistics (Дескриптивные статистики)

Dependent Variable: М1 (Зависимая переменная: М1)
GESCHL ' (Пол)	ALTER (Возраст)	Mean (Среднее значение)	Std. Deviation (Стандартное отклонение)	N
maennlich (Мужской)	bis 30 Jahre (До 30 лет)	16,00	,82	4
31 - 50 Jahre (31 - 50 лет)	14,60	1,14	5
ueber 50 Jahre (Свыше 50 лет)	11,7	2,48	6
Total (Сумма)	13,60	2,69	15
weiblich (Женский)	bis 30 Jahre (До 30 лет)	16,00	1,00	3
31 - 50 Jahre (31 - 50 лет)	15,00	1,41	4
ueber 50 Jahre (Свыше 50 лет)	10,20	1,10	5
Total (Сумма)	13,25	2,93	12
Total (Сумма)	bis 30 Jahre (До 30 лет)	16,00	,82	7
31 - 50 Jahre (31 - 50 лет)	14,78	1,20	9
ueber 50 Jahre (Свыше 50 лет)	10,73	1,95	11

Levene's Test of Equality of Error Variances a (Тест Левене на равенство дисперсии ошибок)

Dependent Variable: М1 (Зависимая переменная: М1)

F	df1	df2	Sig(Значимость)
4,177	5	21	,009

Tests the null hypothesis that the error variance of the dependent variable is equal across groups (Проверяет нулевую гипотезу о том, что дисперсия ошибок зависимых переменных одинакова для всех групп).

a. Design: Intercept+GESCHL+ALTER+GESCHL * ALTER (Компоновка: Отрезок + Пол + Возраст + Пол*Возраст)

К сожалению, тест Левене на равенство дисперсий показывает, значимый результат со значением вероятности ошибки р = 0,009. Это означает, что отсутствует однородность дисперсий между группами, которая наряду с нормальным распределением значений выборки, является основной предпосылкой для возможности проведения дисперсионного анализа.

Традиционная схема дисперсионного анализа (еще раз отметим: проводимого на основе общей линейной модели) показывает незначимое влияние пола (р = 0,761), очень значимое влияние возраста (р = 0,001) и незначимое взаимодействие между обоими переменными (р = 0,611).

Tests of Between-Subjects Effects (Тест межсубъектных эффектов)

Dependent Variable: M1 (Зависимая переменная: М1)

Source (Источник)	Type III Sum of Squares (Сумма квадратов III типа)	Df	Mean Square (Среднее значение квадрата)	F	Sig. (Значи-мость)
Corrected Model (Подпра- вленная модель)	145,833a	5	29,167	12,049	,000
Intercept (Отрезок)	4916,763	1	4916,763	2031,187	,000
GESCHLJOonl	,229	1	,229	,095	,761
ALTER (Возраст)	144,273	2	72,137	29,801	,000
GESCHL * ALTER (Пол'Возраст)	2,446	2	1,223	,505	,611
Error (Ошибка)	50,833	21	2,421
Total (Сумма)	5077,000	27
Corrected Total	196,667	26

a R Squared = ,742 (Adjusted R Squared = ,680) (R-квадрат = 0,742 (смещённый R-квадрат = 0,680))

В случае отсутствия однородности дисперсии границу значимости рекомендуется устанавливать равной не р = 0,05, а р =0,01. Значимое влияние возраста проявляется в любом случае.

Если вы сравните эти результаты с результатами, полученными при методе Фишера (Fisher) (см. гл. 17.1.2), то заметите незначительное отклонение значения р для фактора влияния пол (geschlecht). Далее следует вывод дескриптивных статистик для совокупной выборки и для отдельных слоев факторов.

1. Grand Mean (Общее среднее значение)

Dependent Variable: М1 (Зависимая переменная: М1)
Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
13,828	,307	13,190	14,466

2. GESCHL (Пол)

Dependent Variable: М1 (Зависимая переменная: М1)
GESCHL (Пол)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
maennlich (Мужской)	13,922	,407	13,075	14,769
weiblich (Женский)	13,733	,459	12,779	14,688

3. ALTER (Возраст)

Dependent Variable: М1 (Зависимая переменная: М1)
ALTER (Возраст)	Mean (Среднее значение)	Std. Error (Стандартная ошибка)	95% Confidence Interval (95 % доверительный интервал)
Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
bis 30 Jahre (До 30 лет}	16,000	,594	14,764	17,236
31 - 50 Jahre (31 - 50 лет)	14,800	,522	13,715	15,885
ueber 50 Jahre (Свыше 50 лет)	10,683	,471	9,704	11,663

Затем следует вывод результатов теста Шеффе по сравнению отдельных возрастных групп. На основании частично дублированных результатов, можно сделать вывод, что самая старшая возрастная группа очень значимо отличается от двух других:

Multiple Comparisons (Множественные сравнения)

Dependent Variable: M1 (Зависимая переменная: М1) Scheffe (Шеффе)
(I) ALTER (Возраст)	(J) ALTER (Возраст)	Mean Difference (I-J) (Средняя разность)	Std. Error (Стандар -тная ошибка)	Sig. (Значи-мость)	95% Confidence Interval (95 % доверительный интервал)
Lower Bound (Нижний предел)	Upper Bound (Верхний предел)
bis 30 Jahre (До 30 лет)	31 -50 Jahre (31 -50 лет)	1,22	,784	,317	-.84	3,29
ueber 50 Jahre (Свыше 50 лет)	5,27*	,752	,000	3,29	7,25
31 -50 Jahre (31 -50 лет)	bis 30 Jahre (До 30 лет)	-1,22	,784	,317	-3,29	,84
ueber 50 Jahre (Свыше 50 лет)	4,05*	,699	,000	2,21	5,89
ueber 50 Jahre (Свыше 50 лет)	bis 30 Jahre (До 30 лет)	-5,27*	,752	,000	-7,25	-3,29
31 -50 Jahre (31 -50 лет)	-4,05*	,699	,000	-5,89	-2,21

Based on observed means (Основываясь на наблюдаемых средних значениях). * The mean difference is significant at the ,05 level (Усреднённая разность является значимой на уровне 0,05).

Этот факт подтверждается ещё раз при выводе результатов для рассматриваемых "однородных подгрупп" в другой форме.

М1

Scheffe ^аbс (Шеффе)
ALTER	N	Subset (Подгруппа)
1	2
ueber 50 Jahre (Свыше 50 лет)	11	10,73
31 - 50 Jahre (31 - 50 лет)	9		14,78
bis 30 Jahre (До 30 лет)	7		16,00
Sig. (Значимость)		1,000	,283

Means for groups in homogeneous subsets are displayed (Выводятся средние значения для групп в однородных подгруппах).

Based on Type III Sum of Squares (На основе суммы квадратов III типа).

The error term is Mean Square(Error) = 2,421 (Слагаемое ошибки равно среднему значению квадрата (ошибки) = 2,421).

a. Uses Harmonic Mean Sample Size = 8,699 (Используя среднегармонический размер выборок = 8,699).

b. The group sizes are unequal (Размеры групп не одинаковы). The harmonic mean of the group sizes is used (Используется среднее гармоническое размера групп). Туре I error levels are not guaranteed (Уровень ошибки для I типа не гарантируется).

с. Alpha = ,05

Завершает вывод результатов профильная диаграмма, в которой представлена линейчатая диаграмма возраста отдельно для каждого пола:

Вид графиков для обоих полов почти одинаков, что свидетельствует о незначимом взаимодействии между двумя факторами. Кроме того, наглядно проявляется незначимость различия между двумя полами.

Содержание раздела