16.3 Нелинейная регрессия
Многие связи по своей природе, то есть в реальной жизни, либо являются строго линейными, либо их можно привести к линейному виду. Один пример линейной связи из области медицины был приведен в главе 16.1; ещё одним, уже знакомым нам примером является линейная связь между весом и ростом. При условии наличия лопаточного количества респондентов, на основании измеренных пар значений можно вывести уравнение регрессионной прямой, к которой более или менее приближается '.тожество точек, соответствующие парам значений.
Существуют также линейные связи, следующие непосредственно из физических закономерностей. Так путь s, пройденный, при постоянной скорости с за промежуток времени : рассчитывается по формуле:
s=c•t
Стало быть, путь является линейной функцией времени. А если мы рассмотрим закон свободного падения, то в этом случае расстояние s. которое проходили падающее тело увеличивается пропорционально квадрату времени:
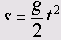
Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряжённом, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
|
s (см)
|
t (сек)
|
|
5
|
1,0
|
|
9
|
1,4
|
|
16
|
1,8
|
|
26
|
2,3
|
|
40
|
2,8
|
|
65
|
3,6
|
|
98
|
4,5
|
Хотя связь между 5 и с и не является линейной, её можно перевести в линейную модель, если взять квадратный корень из обоих сторон закона свободного падения:
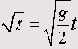
Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
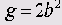
При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь
у = а•е
bx
можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения
ln (у) = ln(a) +
b•x
То есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регресии вычисляются непосредственно, а не определяются с помощью итераций.
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
|
Год
|
Лекала
|
Население
|
|
1790
|
0
|
3,895
|
|
1800
|
1
|
5,267
|
|
1810
|
2
|
7,182
|
|
1820
|
3
|
9,566
|
|
1830
|
4
|
12,834
|
|
1840
|
5
|
1 6,985
|
|
1850
|
6
|
23,069
|
|
1860
|
7
|
31,278
|
|
1870
|
8
|
38,416
|
|
1880
|
9
|
49,924
|
|
1890
|
10
|
62,692
|
|
1900
|
11
|
75,734
|
|
1910
|
12
|
91,812
|
|
1920
|
13
|
109,806
|
|
1930
|
14
|
122,775
|
|
1940
|
15
|
131,669
|
|
1950
|
16
|
150,697
|
|
1960
|
17
|
178,464
|
В таблице приведена численность населения в миллионах и дополнительно количество декад (десятилетий), прошедших с 1790 года.
Зависимость численности населения (переменная pop) от времени
t (выраженного здесь в декадах) часто описывается при помощи следующей формулы:
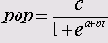
Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3,895 = 200/(1+e
2)
и следовательно
а = ln((200/3,895-1)) = 3,9
Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра
b:
5,267=200/(1+e
3,9+b)
и следовательно
b=ln(5,267-1)-3,9 = -0,3
Определим теперь более точные значения параметров а,
b и с с помощью итераций.
-
Откройте файл usa.sav.
-
Выберите в меню Analyze... (Анализ)
Regression... (Регрессия) Nonlinear... (Нелинейная)
-
В диалоговом окне Nonlinear Regression (Нелинейная регрессия) перенесите переменную pop в поле для зависимых переменных.
-
Щёлкните на поле Model Expression (Модельное выражение) и внесите в него следующую формулу:
c/(l+exp(a+b*dekade))
При вводе формулы можно использовать клавиатуру, находящуюся в диалоговом окне. Диалоговое окно будет выглядеть так, как изображено на рисунке 16.15. Нам осталось только задать начальные значения параметров.
-
Щёлкните на кнопке Parameter... (Параметр)
Вы получите диалоговое окно, в котором сможете задавать начальные значения.
-
Укажите в поле имён имя первого параметра, то есть, к примеру, а, затем щёлкните в поле Starting value (Начальное значение), введите значение 3,9 и щёлкните на Add (Добавить).
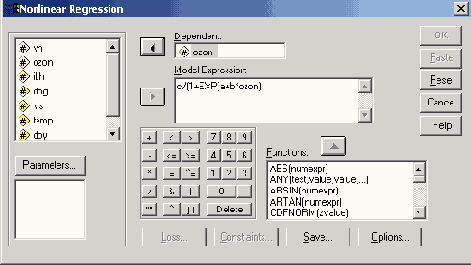
Рис. 16.15: Диалоговое окно Nonlinear Regression (Нелинейная регрессия).
-
Поступите таким же образом с двумя другими параметрами бис (начальные значения —0,3 и 200 соответственно).
-
Покиньте диалоговое окно нажатием Далее.
-
Щёлкните на кнопке Save (Сохранить). Отметьте в диалоговом окне Nonlinear Regression: Save New Variables (Нелинейная регрессия: Сохранить новые переменные) параметры: Predicted Values (Прогнозируемые значения) и Residuals (Остатки). Таким образом, Вы создадите две новые переменные (с именами: pred_ и resid), которые содержат вычисленные значения и остатки для каждого года.
-
Начните расчёт нажатием ОК.
На экране появятся результаты, причём Вы можете заметить, что вывод происходит не в виде привычных современных таблиц. Сначала протоколируется процесс итерации; в рассматриваемом примере для достижения заданного уровня точности понадобилось 10 итерационных шагов. Дополнительно выводятся следующие статистические характеристики:
|
Nonlinear Regression
|
Summary Statistics Dependent Variable POP
|
|
Source
|
DF
|
Sum of Squares
|
Mean Square
|
|
Regression
|
3
|
123048 ,61437
|
41016,20479
|
|
Residual
|
15
|
186,50337
|
12,43356
|
|
Uncorrected Total
|
18
|
123235,11774
|
|
|
(Corrected Total)
|
17
|
53291,50763
|
|
|
R squared = 1Residual SS / CorrectedSS = ,99650
|
Здесь интерес может представлять только член, обозначенный R squared; его следует понимать как часть суммарной дисперсии, которая обусловлена построенной моделью. Вычисленное значение этого параметра, 0.9965, указывает на очень хорошую степень приближения. После этого вывода следует распечатка конечных значений всех трех параметров вместе с соответствующей стандартной ошибкой и доверительным интервалом:
|
Asymptotic 95 % Asymptotic Confidence Interval
|
|
Parameter Estimate
|
Std. Error
|
Lower Upper
|
|
A
|
3,888771432 ,
|
093688592
|
3,6890789254 ,088463938
|
|
|
В
|
-,278834486,
|
015593535
|
-,312071318 - ,245597654
|
|
|
С
|
244,01372955
|
17,974966354
|
205, 70099568 282
|
,32646341
|
Завершает список выводимых результатов корреляционная матрица оценок параметров:
|
Asymptotic
|
Correlation А
|
Matrix of В
|
the
|
Parameter Estimates С
|
|
А
В
С
|
1,0000
-,7243
-,3759
|
-,724:
1,000
,904
|
3
'0
3
|
-,3759
,9043
1,0000
|
Очень высокие абсолютные значения корреляций указывают на то, что модель содержит неоправданно большое количество параметров. В рассматриваемом примере и модель с меньшим количеством параметров даст столь же хорошее приближение.
-
Если Вы хотите визуально сравнить рассчитанные значения с наблюдаемыми, то можете посредством меню Graph... (Графики)
Scatter plots... (Диаграммы рассеяния)
построить многослойную диаграмму рассеяния (Staggered), на которой Вы можете представить переменные pop и pred_ в зависимости от переменной jahr. Также можно поступить и с остатками (переменная rcsid).
Согласно предварительным установкам при расчете нелинейной регрессии происходит минимизация суммы квадратов остатков. При помощи кнопки Loss...(Остаток) можно задать какую-либо другую минимизирующую функцию. Далее при помощи кнопки Constraints...(ограничения) может быть открыто окно, в котором можно задать ограничения для определяемых параметров нелинейной регрессии.
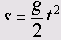 Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряжённом, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
Если Вы захотите проверить это экспериментально, то Вам надлежит сделать серию опытов, в которых будет необходимо бросать некоторый предмет, например, камень, с различной высоты (лучше всего, конечно же, в разряжённом, безвоздушном пространстве) и засекать время падения. Предположим, у Вас получились следующие результаты:
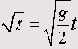 Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
Используя этот коэффициент, можно теперь рассчитать искомое ускорение свободного падения:
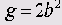 При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь
у = а•еbx
можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения
ln (у) = ln(a) +
b•x
То есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регресии вычисляются непосредственно, а не определяются с помощью итераций.
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
При помощи соответствующих трансформаций в линейную модель можно перевести и другие исходно нелинейные связи. К примеру, очень часто встречающуюся экспоненциальную связь
у = а•еbx
можно преобразовать в линейную при помощи вычисления логарифма от обеих сторон уравнения
ln (у) = ln(a) +
b•x
То есть в данном случае до проведения линейного регрессионного анализа необходимо прологарифмировать независимые переменные.
Связи, которые при помощи соответствующих трансформаций могут быть переведены в линейную связь, называются линейными по существу (Intrinsically Linear Model). Возможность перевода в линейную модель нужно использовать всегда, так как в этом случае параметры регресии вычисляются непосредственно, а не определяются с помощью итераций.
В качестве примера нелинейной по существу связи (Intrinsically Nonlinear Model) можно привести динамику роста населения США (этот пример взят из Справочника по SPSS):
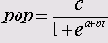 Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3,895 = 200/(1+e2)
и следовательно
а = ln((200/3,895-1)) = 3,9
Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра
b:
5,267=200/(1+e3,9+b)
и следовательно
b=ln(5,267-1)-3,9 = -0,3
Определим теперь более точные значения параметров а,
b и с с помощью итераций.
Общего универсального метода определения параметров подобной нелинейной связи, к сожалению, не существует, поэтому описанная ниже последовательность действий может служить только примером.
В рассматриваемом примере параметр с является амплитудой, так что начальное значение может быть задано немного большим, чем максимум значения pop, то есть приблизительно с = 200.
При помощи значения параметра pop при t = 0 и начального значения параметра с можно получить начальную оценку параметра а:
3,895 = 200/(1+e2)
и следовательно
а = ln((200/3,895-1)) = 3,9
Исходя из значения параметра pop для первой декады, можно вычислить начальное значение параметра
b:
5,267=200/(1+e3,9+b)
и следовательно
b=ln(5,267-1)-3,9 = -0,3
Определим теперь более точные значения параметров а,
b и с с помощью итераций.
