14.6 Отдельный тест по критерию хи-квадрат

С помощью этого теста проверяют, насколько значительно отличаются друг от друга наблюдаемые и ожидаемые частоты переменных, относящихся к номинальной шкале. Как правило, при этом ожидаемая частота подчиняется равномерному распределения; однако в SPSS существует возможность задать соответствующие пропорции.

Одним из примеров ожидаемого равномерного распределения частот являются кости. Предположим, Вы бросили один игральную кость 3000 раз и получили следующее частоты для выпавших очков.

Число очков	Частота	Число очков	Частота
1	511	4	498
2	472	5	513
3	572	6	434

Исходя из предположения об идеальности игральную кость (равной вероятности выпадения любого числа очков), ожидаемая частота для каждого из выпавших чисел составит 3000 / 6 = 500. Необходимо проверить, значимо ли отличаются наблюдаемые частоты от ожидаемых. Данные, а именно переменные augen (число очков) и n (частота), находятся в файле wuerfel.sav. Последнюю переменную следует применить в качестве весовой переменной.

Откройте файл wuerfel.sav.
Сначала выберите в меню Data (Данные) Weight Case (Взвесить наблюдения)
Переменную n объявите частотной (см. гл. 8.7), выберите в меню Analyze (Анализ) Nonparametric Tests (Непараметрические тесты) Chi-Square (Хи-квадрат) Откроется диалоговое окно Chi-Square Test (Тест хи-квадрат) (см. рис. 14.6).
Перенесите переменную augen в поле тестируемых переменных.

Если Вы, как в рассматриваемом примере, хотите подвергнуть анализу все категории тестируемых переменных, то оставьте в разделе Expected range (Ожидаемый диапазон) включённой опцию Get from Data (Из исходных данных); в противном случае у Вас есть возможность ограничить вовлекаемые категории посредством ввода нижней и верхней границ. Так как ожидаемые частоты одинаковы для всех категорий (была принята гипотеза о равномерном распределении), то эта предварительная установка остаётся в силе.

После нажатия кнопки Опции... у Вас появится возможность организовать вывод характеристик дескриптивной статистики и квартилей (что в данном случае является абсолютно бессмысленным).

Запустите расчёт путём нажатия ОК.

В окне просмотра появятся следующие результаты:

Augenzahl (Число очков)

	Observed N (Наблюдаемое N)	Expected N (Ожидаемое N)	Residuals (остатки)
1	511	500,0	11,0
2	472	500,0	-28,0
3	572	500,0	72,0
4	498	500,0	-2,0
5	513	500,0	13,0
6	434	500,0	-66,0
Total (Сумма)	3000

Test Statistics (Статистика теста)

	Augenzahl (Число)
Chi-Square (Хи-квадрат) а	21,236
Df	5
Asymp. Sig. (Статистическая значимость)	,001

a. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 500,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 500,0.)

Получилось очень значимое значение критерия хи-квадрат (р = 0,001). В рассматриваемом случае желателен вывод не абсолютных, а стандартизированных остатков, определяемых по формуле:

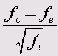
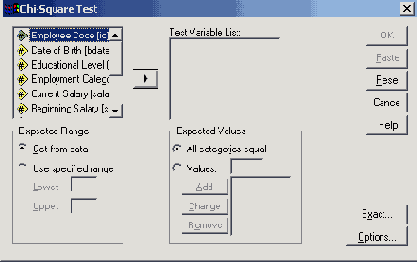
Рис. 14.6: Диалоговое окно СЫ-Square Test (Хи-квадрат-тест)

(см. гл. 11.1). При помощи основополагающего правила, приведенного в главе 8.7.2, можно точно определить те категории, для которых наблюдается значительное отклонение наблюдаемых частот от ожидаемых:

Стандартизированные остатки >= 2,0 указывают на значительное, >= 2,6 на очень значительное и >= 3,3 на сверх значительное отклонение. Если следовать этому правилу, то в экспериментах с игральной костью наблюдается очень значимое превышение количества выпадений 3 очков и очень, очень значимое занижение количества выпадений 6 очков.

Во втором примере, который принадлежит к области ботаники, нужно проверить не равномерное распределение, а наличие распределения подчиняющегося заданному соотношению.

Потомки трёх сортов бобовой культуры были разделены на три типа, которые находятся в соотношении между собой как 1:2:1. Во время некоторого эксперимента, проведенного с сотней таких потомков тип 1 появился 29 раз, тип 2 — 44 раза и тип 3 — 27 раз. Необходимо исследовать значительно ли отклоняется полученное распределение от теоретического распределения 1:2:1.

Данные находятся в файле bohnen.sav, причём переменная typ соответствует типу, а переменная n частоте.

Откройте файл bohnen.sav.
Сначала действуйте так же, как в первом примере, и взвесьте наблюдения с частотной переменной n.
В диалоговом окне Chi-Square Test (тест Хи-квадрат) присвойте переменной typ статус тестируемой переменной.
В поле Expected values (Ожидаемые значения) активируйте в этот раз опцию Values (Значения). Введите числа 1, 2 и 1 в предусмотренное для этого поле, и щёлкните дополнительно на кнопке Add (Добавить).
Запустите расчёт путём нажатия ОК. В окне просмотра появятся следующие результаты:

Тур (Тип)

	Observed N (Наблюдаемое N)	Expected N (Ожидаемое N )	Residual (Остаток)
1	29	25,0	4,0
2	44	50,0	-6,0
3	27	25,0	2,0
Total (Сумма)	100

Test Statistics (Статистика теста)

	Тур (Тип)
Chi-Square (Хи-квадрат) а	1,520
Of	2
Asymp. Sig. (Статистическая значимость)	,468

а. 0 cells (,0%) have expected frequencies less than 5. The minimum expected cell frequency is 25,0. (В 0 ячеек (,0%) ожидаемая частота имеет значение менее 5. Минимальная ожидаемая частота в одной ячейке равна 25,0.)

Ожидаемые частоты выстроены в соответствии с заданным соотношением. На сей раз значимого отклонения наблюдаемых частот от ожидаемых не наблюдается (р = 0,468).

Содержание раздела