Решение оптимизационных задач средствами EXCEL
         

Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений.


С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной или прямой.

Связь исходной и двойственной задач заключается, в част­ности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Переменные двойственной задачи yi

называют объективно обусловленными оценками, или двойственными оцен­ками, или «ценами» ресурсов, или теневыми ценами.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Двойственная задача по отношению к исходной состав­ляется согласно следующим правилам:

1) целевая функция исходной задачи формули­руется на максимум, а целевая функция двойственной задачи— на минимум, при этом в задаче на  максимум все неравенства в функциональных ограничениях имеют вид £, в задаче на минимум — вид ³;

2) матрица А, составленная из коэффициентов при неизвестных в сис­теме ограничений исходной задачи и аналогич­ная матрица    Ат   в  двойственной задаче получаются друг из друга транс­понированием;

3) число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе  двойственной задачи — числу переменных в исходной задаче;

4) коэффициентами при неизвестных в целевой функции   двойственной задачи являются свободные члены в  системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи — коэффициенты при неизвестных в целевой функции исходной задачи;

5) каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записан­ному в виде неравенства £, соответствует переменная, связанная условием неотрицательности. Если функцио­нальное ограничение исходной задачи является равенст­вом, то соответствующая переменная двойственнвой; задачи может принимать как положительные, так и отрицательные значения


Модель исходной (прямой) задачи в общем виде может быть записана следующим образом:

                
                          

Модель двойственной задачи имеет вид:



Две приведенные задачи образуют пару симметричных двойственных задач. Основные утверждения о взаимно двойственных задачах содержатся в двух следующих теоремах.

Первая теорема двойственности.

Для взаимно двойственных задач имеет место один из взаимоисключающих случаев:

1. В прямой и двойственной задачах имеются оптимальные реше­ния, при этом значения целевых функций на оптимальных решениях совпадают: f(x) = g(y).



2. В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограниченна сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым.

           4.Обе из рассматриваемых задач имеют пустые допустимые множества.

Экономический смысл первой теоремы двойственности следующий. План производства Х и набор оценок ресурсов У оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная, при из­вестных заранее ценах продукции  равна затра­там на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов yi. Для всех же других планов Х и У обеих задач прибыль от продукции всегда меньше (или равна) стоимости затраченных ресурсов:

f(X) < g(Y}, т. е. ценность всей выпущенной продукции не превосходит суммарной оценки имеющихся ресурсов. Зна­чит величина g(Y) - f(X) характеризует производственные потери в зависимости от рассматриваемой производственной программы и выбранных Оценок ресурсов.

Из первой теоремы двойственности следует, что при оп­тимальной производственной программе и векторе оценок ресурсов производственные потери равны нулю.

 Вторая теорема двойственности



(теорема о дополняющей нежесткости)

Пусть X=(x1,x2,...xn) - допустимое решение прямой задачи, а Y= (y1,y2,...ym) - допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответственно прямой и двойственной задач необходимо и достаточно, чтобы выполнялись следующие соотношения:

                                                      *

                                                      **

Условия (*) и (**) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

Из второй теоремы двойственности в данном случае следуют такие требования на оптимальную производственную программу X=(X1,X2,...,Xn) и оптимальный вектор оценок Y=(Y1,Y2,...,Ym):

     (4)

        (5)

Условия (4) можно интерпретировать так: если оценка yi единицы ресурса i-го вида положительна, то при оптимальной производственной программе этот ресурс используется полностью, если же ресурс используется не полностью, то его оценка равна нулю. Из условия (5) следует, что если j-й вид продукции вошел в оптимальный план, то он в оптимальных оценках неубыточен, если же j-й вид продукции убыточен, то он не войдет в план, не будет вы­пускаться.

Рассмотрим еще одну теорему, выводы которой будут использованы в дальнейшем.

Теорема об оценках.

Значения переменных Yi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi системы ограничений-неравенств прямой задачи на величину

                                                                           

Решая ЗЛП  симплексным методом, мы одновременно решаем двойственную ЗЛП. Переменные двойственной задачи yi называют объективно обусловленными оценками.

Рассмотрим экономическую интерпретацию двойственной задачи на примере задачи оптимального использования ресурсов.

Пример. Сформулируем экономико-математическую модель двойственной задачи к задаче о коврах.

Прямая задача:

f(x) = 3Х1 +4Х2 +3Х3 +1Х4

Ограничения по ресурсам



7Х1 +2Х2

+2Х3 +6Х4
80

5Х1 +8Х2

+4Х3 +3Х4
480

2Х1 +4Х2

+Х3 +8Х4
130

Х1, Х2, Х3, Х4
0

Количество неизвестных в двойственной задаче равно числу функциональных ограничений в исходной задаче. В исходной задаче три

ограничения – по труду, по сырью и по оборудованию. Следовательно, в двойственной задаче – три

неизвестных:

Y1

– двойственная оценка ресурса труд, или «цена» труда;

Y2

– двойственная оценка ресурса сырье, или «цена» сырья;

Y3

– двойственная оценка ресурса оборудование, или «цена» оборудования.

Целевая функция двойственной задачи формулируется на минимум. коэффициентами при неизвестных в целевой функции   двойственной задачи являются свободные члены в  системе ограничений исходной задачи.

g
  = 80 ´Y1 + 480´Y2 + 130´Y3  ® min

Необходимо найти такие “цены” на ресурсы (Yi), чтобы общая стоимость  используемых ресурсов была минимальной.

Ограничения.

число ограничений в системе  двойственной задачи равно числу переменных в исходной задаче. В исходной задаче четыре

переменных, следовательно, в двойственной задаче четыре ограничения. правыми частями в ограничениях двойственной задачи являются коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничения определяет стоимость ресурсов, затраченных на производство единицы продукции.  Каждое ограничение соответствует определенному виду продукции.

7 ´Y1 + 5´Y2 + 2´Y3 ³ 3

2 ´Y1 + 8´Y2 + 4´Y3 ³ 4

2 ´Y1 + 4´Y2 + 1´Y3 ³ 3

6 ´Y1 + 3´Y2 + 8´Y3 ³ 1

Y1 ,Y2 ,Y3 ³ 0

Решение двойственной задачи можно найти  в отчете Поиска решений.

 Отчет по устойчивости. Теневые цены ресурсов труд, сырье и оборудование соответственно равны 4/3, 0, 1/3 или  в десятичных дробях 1.3333,  0,   0.3333.

Отчет по устойчивости
Изменяемые ячейки
Результ.

 Нормир.

 Целевой

 Допустимое

 Допустимое
Ячейка

 Имя

 Значение

 Стоимость

 Коэффициент

 Увеличение

 Уменьшение
$B$3

 Значение Х1

 0

 -7

 3

 7

 1E+30
$C$3

 Значение Х2

 30

 0

 4

 8

 1
$D$3

 Значение Х3

 10

 0

 3

 1

 1.75
$E$3

 Значение Х4

 0

 -9.667

 1

 9.667

 1E+30
Ограничения
Результ.

 Теневая

 Ограничение

 Допустимое

 Допустимое
Ячейка

 Имя

 Значение

 Цена

 Правая часть

 Увеличение

 Уменьшение
$F$7

 труд левая часть

 80

 1.333

 80

 150

 15
$F$8

 сырье левая часть

 280

 0

 480

 1E+30

 200
$F$9

 Оборудование левая часть

 130

 0.333

 130

 30

 90
<


Проведем анализ полученного оптимального решения исходной задачи с помощью двойственных оценок.

1)    Анализ использования ресурсов в оптимальном плане выполняется с помощью соотношений второй теоремы двойственности.



Ресурсы труд и оборудование имеют отличные от нуля оценки 4/3 и 1/3 – эти ресурсы полностью используются в оптимальном  плане, являются дефицитными, сдерживающими рост целевой функции. Правые части этих ограничений равны левым частям.

7Х1 +2Х2 +2Х3

+6Х4
80

2Х1 +4Х2 +Х3

+8Х4
130

7´0 +2´30 +2´10 +6´0=80=80

2´0 +4´30 +1´10 +8´0=130=130

Ресурс сырье используется не полностью (280<480), поэтому имеет нулевую двойственную оценку (Y2=0).

5Х1 +8Х2 +4Х3

+3Х4
480

5´0 +8´30 +4´10 +3´0=280<480

Этот ресурс не влияет на план выпуска продукции.

Общая стоимость используемых ресурсов при выпуске 30 ковров второго вида и 10 ковров третьего вида составит 150 тыс. руб.

g
= 80 ´Y1 + 480´Y2 + 130´Y3 =80 ´4/3 +480´0+130´1/3 =150 тыс. руб.

По условию (4) не использованный полностью в оптимальном плане ресурс по­лучает нулевую оценку. Нулевая оценка ресурса свидетель­ствует о его не дефицитности. Ресурс не дефицитен не из-за его неограниченных запасов (они ограничены величиной bi), а из-за невозможности его полного использования в опти­мальном плане. Так как суммарный расход недефицитного ресурса меньше его общего количества, то план производст­ва им не лимитируется. Данный ресурс не препятствует и дальше максимизировать целевую функцию f(X).

Заметим, что ценность различных видов ресурсов нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере,  имеющей экономическую природу, которая характеризует ценность ресурса только относительно полу­ченного оптимального решения.

2) Анализ эффективности отдельных вариантов плана выполняется на основе соотношений из 2 теоремы двойственности.





Если изделие вошло в оптимальный план (Xj  >0), то в двойственных оценках оно не убыточно, то есть, стоимость ресурсов, затраченных на производство единицы изделия равна его цене.  Такие изделия эффективны, выгодны с точки зрения принятого критерия оптимальности. В нашей задаче это ковры второго и третьего видов.

Если стоимость ресурсов, затраченных  на производство одного изделия больше его цены, то это изделие не войдет в оптимальный план из-за его убыточности. В  нашей задаче в план выпуска  не вошли ковры первого и четвертого видов, потому что затраты по ним превышают цену на 7 (10-3) тыс. руб. и 9.666 (10.666-1) тыс. руб. соответственно. Это  можно подтвердить, подставив в ограничения двойственной задачи оптимальные значения вектора Y.

7 ´4/3 + 5´0+ 2´1/3=30/3=10 >3

2 ´4/3 + 8´0+ 4´1/3=12/3= 4= 4

2 ´4/3 + 4´0+ 1´1/3= 9/3= 3= 3

6´4/3 + 3´0+ 8´1/3=32/3= 10.666 > 1

Разницу между правыми и левыми частями ограничений двойственной задачи можно найти в Отчете по устойчивости в столбце Нормируемая стоимость.

2)    Анализ влияния изменения правых частей ограничений на значения целевой функции (Чувствительность решения к изменению запасов сырья).

Предположим, что запас сырья ресурса «труд» изменился на 12 единиц, т. е. теперь он составляет 80 + 12 = 92 единиц. Из теоремы об оценках, известно, что колеба­ние величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi

в случае, когда при изменении величин bi

значения переменных yi

в оптималь­ном плане соответствующей двойственной задачи остаются неизменными. В нашей задаче увеличение запасов ресурса «труд»  приведет к увеличению значения целевой функции на 16 тыс. руб.(Df(x)= D b1´ y1

=12´4/3 = 16). Для двойственных оценок оптимального плана весьма существенное значение имеет их предельный характер. Точной мерой влияния ограничений на функционал оцен­ки являются лишь при малом приращении ограничения. Известно, что оценки не меняют своей величины, если не меняется набор векторов, входящих в базис оптимального плана, тогда как интенсивность этих векторов (значения неиз­вестных) в плане могут меняться.



  Поэтому необходимо знать такие интервалы изменения каждого из свободных членов системы ограниче­ний исходной ЗЛП, или интервалы устойчивости двойственных оценок, в которых оптимальный план двойст­венной задачи не менялся бы. Эту информацию можно получить  из Отчета по устойчивости. В нашей задаче  в ниже приведенном фрагменте отчета видно, что  запасы дефицитных ресурсов труд и оборудование могут быть, как уменьшены, так и увеличены,  увеличение запаса ресурса сырье не повлияет на план выпуска продукции.

Ограничение

 Допустимое

 Допустимое
правая часть

 Увеличение

 уменьшение
80

 150

 15
480

 1E+30

 200
130

 30

 90
После увеличения запаса ресурса труд до 92 чел/ часов было получено новое решение задачи. Изменение запасов ресурсов в пределах интервалов устойчивости двойственных оценок привело не только к изменению значения целевой функции на 16 тыс. руб., но и к изменению плана выпуска. При этом структура плана не изменилась - изделия, которые были убыточны не вошли и в новый план выпуска, т.к. цены на ресурсы не изменились. Новый план выпуска составляет 28 ковров второго вида и 18 ковров третьего вида. Изменение общей стоимости продукции на 16 тыс. руб. (24-8=16) получено за счет уменьшения на 2 единицы ковров второго вида по цене 4 тыс. руб.  (4 тыс. руб.´(28-30)= -8 тыс. руб.) и увеличения на 8 единиц ковров третьего вида по цене 3 тыс. руб. (3 тыс. руб.´(18-10)= 24 тыс. руб.).

Отчет по устойчивости 2
Изменяемые ячейки
Результ.

 Нормир.

 Целевой

 Допустимое

 Допустимое
Ячейка

 Имя

 значение

 Стоимость

 коэффициент

 увеличение

 уменьшение
$B$3

 значение Х1

 0

 -7

 3

 7

 1E+30
$C$3

 значение Х2

 28

 0

 4

 8

 1
$D$3

 значение Х3

 18

 0

 3

 1

 1.75
$E$3

 значение Х4

 0

 -9.667

 1

 9.667

 1E+30
Ограничения
Результ.

 Теневая

 Ограничение

 Допустимое

 Допустимое
Ячейка

 Имя

 значение

 цена

 правая часть

 увеличение

 уменьшение
$F$7

 труд левая часть

 92

 1.333

 92

 138

 27
$F$8

 сырье левая часть

 296

 0

 480

 1E+30

 184
$F$9

 оборудование левая часть

 130

 0.333

 130

 54

 84
<


 

Задача 5.

Задача о размещении производственных заказов

в планируемом периоде необходимо обеспечить производство 300 тыс. однородных новых изделий, которые могут выпускаться на четырех филиалах предприятия. Для освоения этого нового вида изделий выделены капитальные вложения в размере 18 млн. руб.. Разработанные для каждого филиала предприятия проекты освоения нового вида изделия характеризуются величинами удельных капитальных вложений и себестоимостью единицы продукции в соответствии с таблицей.

Необходимо найти такой вариант распределения объемов производства продукции и ка­питальных вложений по филиалам, при котором суммарная стоимость изделий будет минимальной.

Таблица

Показатель

 Филиал предприятия
1

 2

 3

 4
Себестоимость производства изделия, руб.

 83

 89

 95

 98
Удельные капиталовложения, руб.

 120

 80

 90

 40
В результате решения получен  план распределения объемов производства по филиалам предприятия 

Филиал предприятия
1

 2

 3

 4
0

 100

тыс. штук

 200

тыс. штук

 0
Требуется:

1)  Сформулировать экономико-математическую модель прямой и двойственной задачи.

2)  Найти оптимальный план двойственной задачи, используя теоремы двойственности.


 Графический метод решения задач линейного программирования.


Наиболее простым и  наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.

Рассмотрим задачу ЛП в стандартной форме записи:

                

                          

Положим n=2, т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).

Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой  ai1 x1 + ai2

x2  =  bi   , i=1,2,…m. Условия неотрицательности определяют полуплоскости, соответственно, с граничными прямыми x1=0,x2 =0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.

Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника  решений.

           Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х1+3х2£

12.  Во-первых, построим прямую 2х1+3х2=12.  Эта прямая проходит через точки (6, 0) и (0, 4).  Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет

неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим х1=х2=0 в неравенство 2х1+3х2£12. Получим 2´0+3´0£12.  Данное утверждение является верным, следовательно, неравенству 2х1+3х2£12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на рис.1.
Рис. 1.  Неравенству 2х1+3х2£12 соответствует нижняя полуплоскость.

Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.

Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей,  каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет

.

условиям неотрицательности (xj ³0, j=1,…,n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи.

Для нахождения экстремального значения целевой функ­ции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т.е.

.

Этот вектор показывает направление наискорейшего изменения це­левой функции. Прямая
, перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”.

Меняя значение “a”,  получим семейство параллельных прямых, каждая из которых является линией уровня.

 Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – убывает.

С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Графический метод решения ЗЛП состоит из следующих этапов.

1.      Строится многоугольная область допустимых решений ЗЛП – ОДР,

2.      Строится вектор-градиент ЦФ в  какой-нибудь точке Х0  принадлежащей ОДР –



               
.

3.  Линия уровня C1x1+C2x2 = а (а–постоянная величина) - прямая, перпендикулярная  вектору –градиенту
 – передвигается в направлении  этого вектора в случае максимизации f(x1,x2)   до тех пор, пока не покинет пределов ОДР. Предельная точка  (или точки) области при этом движении и является точкой максимума f(x1,x2).

 4.  Для нахождения ее координат достаточно решить два уравнения прямых, получаемых  из соответствующих ограничений и дающих в пересечении точку максимума.  Значение f(x1,x2), найденное в получаемой точке, является максимальным.

При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1,x2)  не существует.

Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.

Рассмотрим графическое решение задач линейного программирования на следующем примере.

Задача 1. о планировании выпуска продукции пошивоч­ному предприятию. (Задача о костюмах).

Намечается выпуск двух видов костюмов - мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм - 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Tребуется определить,  сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского - 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

Модель задачи.

Введем следующие обозначения: х1 - число женских костюмов;     x2 - число мужских костюмов.

Прибыль от реализации женских костюмов составляет 10х1, а от реализации мужских 20х2, т.е. необходимо максимизировать целевую функцию



f(x) = 10´

х1 + 20´  х2 -> max.

Ограничения задачи имеют вид:

      х1    +        х2 £ 150

2
 х1 + 0.5
 х2 £  240

х1 + 3.5
 х2 £  350

         х2³ 60      

          х1 ³ 0

Первое ограничение по труду  х1   +  х2 £

150. Прямая х1   +  х2 = 150 проходит через точки (150, 0) и (0, 150).



Рис. 2. Решением первого неравенства является нижняя полуплоскость.

Второе ограничение по лавсану 2
 х1 + 0.5
 х2 £  240.           Прямая 2
 х1 + 0.5
 х2 =  240  проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х1 + 3.5
 х2 £  350.  Добавим четвертое ограничение по количеству мужских костюмов х2  ³ 60.  Решением этого неравенства является полуплоскость, лежащая выше прямой х2  = 60. На рис.3. заштрихована область допустимых решений.





 

Рис. 3.       Заштрихована область допустимых решений.

 



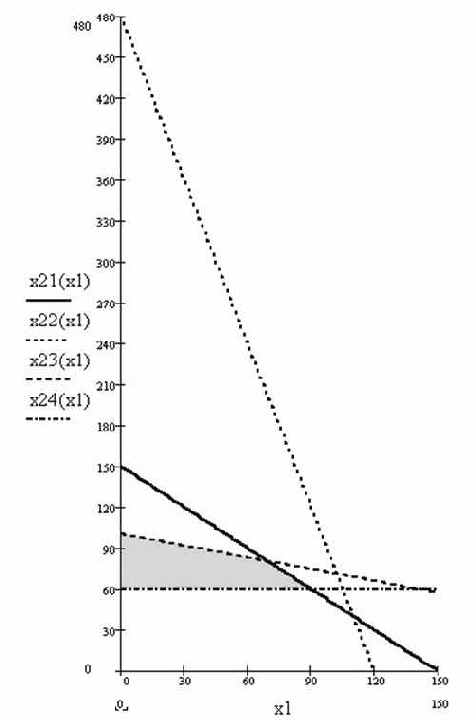
Для определения направления движения к оп­тимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е.
= (10;20).

Что бы построить этот вектор, нужно соединить точку (10;20) с началом координат. При макси­мизации целевой функции необходимо двигаться в направ­лении вектора-градиента, а при минимизации — в противо­положном направлении. Для удобства можно строить век­тор, пропорциональный вектору Ñ. Так, на рис. 2.1.6. изобра­жен вектор  градиент (30;60).

В нашем случае движение линии уровня будем осущест­влять до ее выхода из области допустимых решений. в крайней, угловой  точке достигается максимум целевой функции. Для нахождения координат этой точки  достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:  х1    + 3.5
 х2 =  350

                                                             х1   +  х2

= 150 . 

Отсюда лег­ко записать решение исходной ЗЛП: max f(x) = 2300 и дости­гается при x1=70 и x2=80 (рис. 4.)





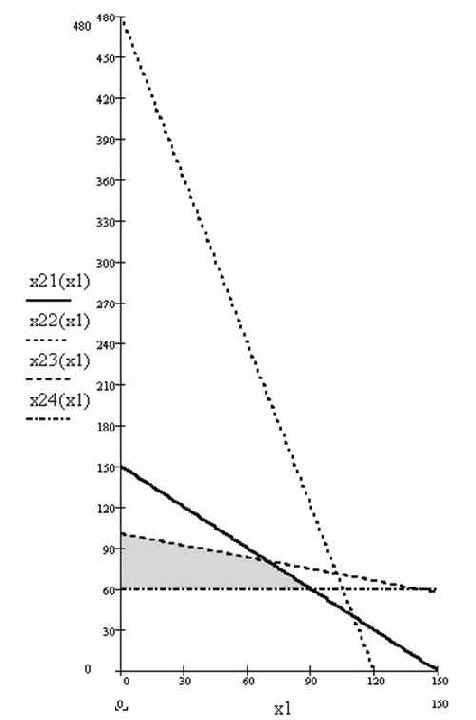
Рис.4. Максимум целевой функции достигается в точке (70, 80).



Х2=80

F(x)=2300

">
 

Задача 2. Для изготовления двух видов продукции А1 и А2

используют три вида ресурсов S1, S2, S3,

запасы которых  составляют 18, 16 и 5 усл.ед. Расход ресурсов на 1 ед. продукции приведен в таблице:

Виды ресурсов

 Запасы ресурсов

 Расходы ресурсов на 1 изд.
А1

 А2

Общая задача оптимизации


Целью работы коммерческой фирмы является получение прибыли. Любое управленческое решение (будь то решение о количестве приобретаемого товара, или решение о назначении цены на реализуемый товар, или решение о подаче рекламы в газету и т.д.) будет влиять на прибыль в большую или меньшую сторону. Эти решения являются оптимизационными, то есть всегда существует возможность выбрать лучшее решение из нескольких возможных. Представим себе, что все управленческие решения принимаются наилучшим образом. То есть, все параметры, на которые может влиять фирма, являются оптимальными. Тогда фирма будет получать максимальную прибыль (больше получить при данных условиях невозможно). Для того чтобы  определить, насколько управленческие решения, принимаемые работниками фирмы оптимальны, можно использовать методы математического программирования.

В экономике оптимизационные задачи возникают в связи с мно­гочисленностью возможных вариантов функционирования кон­кретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуе­мому соответствующей целевой функцией (например, иметь мини­мум затрат, максимум продукции).

Оптимизационные модели отражают в математической форме смысл экономической задачи, и отличительной особенностью этих моделей является наличие условия нахождения оптимального ре­шения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяю­щих условиям задачи, и обеспечивают выбор оптимального реше­ния, отвечающего критерию оптимальности.

В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции f (х1, х2, ..., хn) при условиях gi(х1, х2, ..., хn) £ bi;  (i

=1,2,…m), где f

и gi; – заданные функции, а bi – некоторые действительные числа. 

задачи математического программирования делятся на задачи линейного и нелинейного программирования. если все функции f и gi


линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования. 

В общем виде задача линейного программирования (ЗЛП) ставится следующим образом:

Найти вектор
, максимизирующий линейную форму

                                 (1)

и удовлетворяющий условиям

                                        (2)

      
                                (3)

Линейная функция
 называется целевой функцией задачи. Условия (2)  называются функциональными, а (3) - прямыми ограничениями задачи.

Вектор
, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.

Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f(x), называется оптимальным планом задачи

,

где
 - оптимальное решение ЗЛП. Будем считать, что ЗЛП записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательны.

На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным:  модели определения оптимальной производственной программы, модели оптимального смешивания компонентов, оптимального раскроя, оптимального размещения предприятий некоторой отрасли на определенной территории, модели формирования оптимального портфеля ценных бумаг, модели транспортной задачи.


Прибыль


2 руб.

3 руб.

Необходимо составить такой план производства продукции, который обеспечит наибольшую прибыль от ее реализации.

Составим экономико-математическую модель (ЭММ)

задачи.

Пусть надо выпустить изделий A1 -  x1 шт., а изделий А2 - x2 шт. Тогда прибыль  F = 2x1

+ 3x2 Þ max

x1 + 3x2 £

 18
2x1 + x2 £

 16
x2 £

 5
x1 ³ 0,

 x2 ³ 0

Решим задачу графически.

1)

 x1 + 3x2 £ 18
 

 x1 + 3x2 = 18             (0; 6) (18; 0)
 

 к.т. (0; 0), 0 + 3*0 < 18 (в) – входит
2)

 2x1 + x2 £ 16
2x1 + x2 = 16             (0; 16) (8; 0)
к.т. (0; 0), 2*0 + 0 < 16 (в) – входит
3)

 x2 £ 5
x2 = 5,  x2 < 5 - ниже прямой
4)

 x1 ³ 0 - правее ОX2
5)

 x2 ³ 0 - выше ОX1
  Линия уровня

 F = 2x1 + 3 x2     F = 0
 

 2x1 + 3x2 = 0  (0; 0) (3; -2)

q = {2; 3} - указывает направление возрастания F.

max F достигается в т. С

т.С

 x1 + 3 x2 = 18

 Þ -

  2 x1 + 6 x2 = 36

 Þ

 5 x2 = 20

 Þ

2x1 + x2 = 16

  2 x1 + x2 = 16

  x1 + 3 x2 = 18
Þ

 x2 = 4  
 x1 = 6



 Решение


1) Экономико-математическая модель исходной задачи.

  Xi - объем выпускаемой продукции на i-м филиале предприятия.

= 83X1+89X2+95X3+98X4

-> min,

Ограничения

 X1+X2+X3+X4 ³ 300                      (тыс. штук)

120X1+80X2+50X3+40X4

 £   18     (млн.руб.),

X1,2,3,4 ³0.

 

83

 89

 95

 98
Y1

 1

 1

 1

 1

 300000
Y2

 120

 80

 50

 40

 18000000

Экономико-математическая модель двойственной задачи.

Y1

- двойственная оценка выпускаемой продукции, которая может быть ценой изделия;

Y2

- двойственная оценка капитальных вложений, которая может быть представлена как коэффициент эффективности капитальных вложений.

g

  =300000 Y1+18000000

Y2 -> mах

1 Y1+120Y2

£  83

1 Y1+  80Y2   £  89

1 Y1+  50Y2  £  95

1

Y1+  40Y2  £  98

2) для определения оптимального плана двойственной задачи воспользуемся соотношениями второй теоремы двойственности.  Если какое-либо ограничение исходной задачи выполняется как строгое неравенство, то соответствующая двойственная оценка равна нулю

(

).

0+100000+200000+0 = 300000

120´0+80´100000+50´200000+4´0  =  18000000    

Если какая-либо переменная исходной задачи входит в оптимальный план,  то соответствующее ограничение двойственной задачи выполняется как строгое равенство

).

В нашей задаче Х2=100000>0 и Х3=200000>0, поэтому второе и третье ограничения двойственной задачи обращаются в уравнения, решая которые найдем Y1и  Y2   .

   1 Y1+  50Y2  =  95       Y1=    105  - средняя цена изделия

      1 Y1+  80Y2   =  89       Y2   =  - 0.2 -

двойственная оценка капитальных вложений.

105 =95 +50 ´0.2 = 105

105 =89+ 80´0.2 = 105

На втором и третьем филиалах выпускать новые изделия целесообразно так как  затраты на его освоение и выпуск не превышают цену изделия.

Проверим выполнение первой теоремы двойственности.

g

  =300000 Y1+18000000 Y2 = 300000 ´105+18000000´(–0.2)  = 279 000 000

= 83X1+89X2+95X3+98X4 =83´0+89´100000+95´200000+98´0  = 279 000 000.

Полученные оптимальные планы говорят о том, что в первом и четвертом филиалах размещать заказы по выпуску новых изделий невыгодно (Х1=0 и Х4=0),  так как затраты на производство единицы изделия в этих филиалах больше цены изделия.

 1 ´Y1+  120´Y2  =  83       Y1=    105       105+  120´(-0.2)  <  95     105< 95+24 = 119

 1 ´Y1+    40´Y2   =  98        Y2   =  - 0.2     105+    40´(-0.2)   <  89       105<98+8 = 106.

 



Решение систем линейных уравнений методом жордана - гаусса


Пример 1.     Решить методом Жордана-Гаусса систему линейных уравнений:

            а)  Х1 + Х2 + 2Х3

= -1

               2Х1 -  Х2 + 2Х3

= -4

               4Х1 + Х2 + 4Х3

= -2

Решение:

 Составим расширенную матрицу

1 Итерация.

В качестве направляющего элемента выбираем элемент

. Преобразуем первый столбец в единичный. Для этого к второй и третьей строкам прибавляем первую строку, соответственно умноженную на -2  и -4. Получим матрицу:

На этом первая итерация закончена.

2 Итерация.

Выбираем направляющий элемент

. Так как
, то делим вторую строку на -3. Затем умножаем вторую строку на 1 и 3 и складываем соответственно с первой и третьей строками. Получим матрицу:

3 Итерация.

Выбираем направляющий элемент

. Так как
, то делим третью строку на -2. Преобразуем третий столбец в единичный. Для этого умножаем третью строку на -4/3 и -2/3 и складываем соответственно с первой и второй строками. Получим матрицу:

откуда Х1 = 1,  Х2 = 2,  Х3

= -2.

 

Пример 2.  Решить методом Жордана - Гаусса систему линейных уравнений:

              Х1 + 2Х2 + 2Х3

+22Х4 –4Х5= 11

              Х1 +2Х2 + Х3

+16Х4–4Х5= 9

              Х1 + Х2 + Х3

+12Х4 -2Х5= 6

Решение:

Составим расширенную матрицу

1 Итерация.

В качестве направляющего элемента выбираем элемент

. Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на -1. Получим матрицу:

На этом первая итерация закончена.

2 Итерация.

Выбираем направляющий элемент

. Умножаем  третью строку на -1. Преобразуем второй столбец в единичный. Для этого к первой строке прибавляем третью строку, соответственно умноженную на -2.

Получим матрицу:

3 Итерация.

Выбираем направляющий элемент

. Так как
, то умножаем вторую строку на –1. Преобразуем третий столбец в единичный. Для этого вторую строку складываем  с третьей строкой. Получим матрицу:

Х1

 Х2

 Х3

 Х4

 Х5

  
1

 2

 2

 22

 -4

 1

 0

 0

 11
1

 2

 1

 16

 -4

 0

 1

 0

 9
1

 1

 1

 12

 -2

 0

 0

 1

 6
1

 2

 2

 22

 -4

 1

 0

 0

 11
1

 0

 0

 -1

 -6

 0

 -1

 1

 0

 -2
0

 -1

 -1

 -10

 2

 -1

 0

 1

 -5
1

 0

 0

 2

 0

 -1

 0

 2

 1
2

 0

 0

 -1

 -6

 0

 -1

 1

 0

 -2
0

 1

 1

 10

 -2

 1

 0

 -1

 5
1

 0

 0

 2

 0

 -1

 0

 2

 1
3

 0

 0

 1

 6

 0

 1

 -1

 0

 2
0

 1

 0

 4

 -2

 0

 1

 -1

 3
1

 0

 0

 2

 0

 -1

 0

 2

 1
0

 1

 0

 4

 -2

 0

 1

 -1

 3
0

 0

 1

 6

 0

 1

 -1

 0

 2
<
Исходная система эквивалентна следующей системе уравнений:
                Х1 + 2Х4 = 1
                Х2 +4Х4 -2Х5= 3
                Х3 +6Х4= 2
Система уравнений имеет бесконечное множество решений.
             Общее решение имеет вид:
             Х1 =  1-2Х4
                    Х2 = 3-4Х4 +2Х5
             Х3 = 2-6Х4.
      переменные Х1, Х2, Х3
являются основными
(или базисными). Любое частное решение получается из общего путем придания конкретных значений свободным переменным. Если свободные переменные Х4 и Х5 положить равными нулю, то получим первое базисное решение Х1 =  1,      Х2 = 3,   Х3 = 2, Х4 = 0,   Х5=0.
Первое базисное решение имеет вид: (1,3,2,0,0).
Общее число групп основных переменных, т.е. базисных решений не более, чем
=
=
.
Если все компоненты базисного решения неотрицательны, то такое решение называется опорным.

Симплексный метод решения задачи линейного программирования


Для решения ЗЛП существует универсальный метод  – метод последовательного улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом (М-метод). 

Выбор конкретной вычислительной процедуры осуществляется после приведения исходной ЗЛП к каноническому виду (КЗЛП):

                             

В теории линейного программирования (ЛП) показано, что оптимальное решение ЗЛП связано с угловыми (крайними) точками многогранника решений, которым отвечают опорные планы (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых  векторов, содержащихся в данной системе из n векторов  А1, А2,…, Аn. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний Сnm.

Задача 3. Получить решение по модели задачи об оптимальном использовании ограниченных ресурсов (решить ЗЛП):

                                                          

     

Приведем задачу к каноническому виду путем введения дополнительных переменных  x 3   и x4:

                                                                   

  

Найдем все опорные планы КЗЛП. Используя метод Жордана-Гаусса выписываем все базисные решения системы уравнений:

                                                                     

Последовательно будем иметь:

Х1

= (0,0,300,150);      Х2= (150,0,150,0);     Х3= (0,150,-150,0);       Х4= (75,75,0,0); Х5= (300,0,0,-150);    Х6= (0,100,0,50).

Среди этих базисных решений четыре опорных:

Х1

= (0,0,300,150);       Х2= (150,0,150,0);          Х4= (75,75,0,0);      Х6= (0,100,0,50).

Указанным опорным планам на рис.5 отвечают соответственно следующие угловые точки и значения ЦФ в них:

А(0,0) и f(0,0)=0; Д(150,0) и f(150,0)=300; С(75,75) и f(75,75)=375; В(0,100) и f(0,100)=300.

Согласно теории ЛП оптимальное решение содержится среди опорных планов.

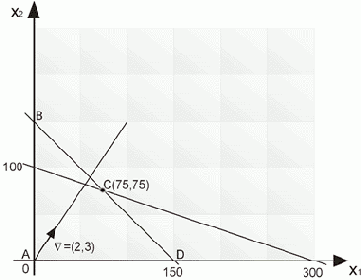
Рис.5

Таким образом, максимальное значение, равное 375, целевая функция f (x1,x2) достигает на опорном плане Х4= (75,75,0,0), т.е. оптимальное решение рассматриваемой ЗЛП:  x1  = 75,  x2 = 75.


Понятно, что при больших m и n найти оптимальный план, перебирая указанным выше способом (прямым перебором) все опорные ЗЛП весьма трудно. Поэтому необходимо иметь схему, позволяющую осуществлять упорядоченный переход от одного опорного плана к другому. Такой схемой является симплексный метод.

Симплекс-метод с естественным базисом

Для применения симплекс-метода с естественным базисом КЗЛП должна содержать единичную подматрицу размером mxm – в этом случае очевиден начальный опорный план (неотрицательное базисное решение системы ограничений КЗЛП).

Для определенности предположим, что первые  m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный опорный план очевиден  – (b1, b2 ,…, bm ,0,…,0).

Проверка на оптимальность опорного плана проходит с помощью признака оптимальности, переход к другому опорному плану проводится с помощью преобразований Жордана-Гаусса при использовании математического признака оптимальности. Полученный опорный план снова проверяется на оптимальность и так далее. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получается оптимальный опорный план и соответствующее ему оптимальное значение ЦФ.

Математический признак оптимальности состоит из следующих двух теорем:

1.      Если для всех векторов А1, А2,…, Аn выполняется условие

                         
  где  
,

то полученный опорный план является оптимальным.

2.      Если для некоторого вектора, не входящего в базис, выполняется условие          
, то можно получить новый опорный план, для которого значение ЦФ будет больше исходного, при этом могут быть два случая:

-          если все компоненты вектора, подлежащего вводу в базис, неположительны, то ЗЛП не имеет решения (конечного оптимума нет);

-          если имеется хотя бы одна положительная  компонента у вектора, подлежащего вводу в базис, то можно получить новый опорный план.



На основании признака оптимальности в базис вводится вектор Ак , давший минимальную отрицательную величину симплекс разности:

                                     
 

Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор Аr, который дает минимальное положительное оценочное отношение

                       
         

Строка Аr

называется направляющей, столбец Ак и элемент ar к – направляющими.

Элементы направляющей строки в новой симплекс-таблице вычисляются по формулам:

                   
        

 а элементы  i-й  строки – по формулам:

             
 

Значения нового опорного плана рассчитываются по формулам:

  
 для  i = r ;         
 

Процесс решения продолжают либо до получения оптимального плана, либо до установления неограниченности ЦФ. Если среди симплекс-разностей (оценок) оптимального плана нулевые только оценки, соответствующие базисным векторам, то это говорит о единственности оптимального плана. Если же нулевая оценка соответствует вектору, не входящему, то в общем случае это означает, что оптимальный план не единственный.

Примечание. Для использования приведенной процедуры к минимизации линейной функции  f (x1,x2,…, xn) следует искать максимум  - f (x1,x2,…, xn), затем полученный максимум взять с противоположным знаком. Оптимальное решение то же.

Пример.

Получить решение по модели: 

 

Эта задача (модель) линейного программирования, приведем ее к каноническому виду путем введения дополнительных переменных  x 3   и x4:

                                                           
               

КЗЛП имеет необходимое число единичных столбцов, т.е. обладает очевидным начальным опорным планом (0,0,300,150). Решение осуществляется симплекс-методом с естественным базисом с оформлением расчетов в симплекс-таблицах:

Номер

    


В

 2

 3

 0

 0
симплекс-

 Базис

 план








Q
таблицы


А3

 0

 300

 1

 3

 1

 0

 100
0

 А4

 0

 150

 1

 1

 0

 1

 150
f(x)

 0

 -2

 -3

 0

 0


А2

 3

 100

 1/3

 1

 1/3

 0

 300
I

 А4

 0

 50

 2/3

 0

 -1/3

 1

 75
f(x)

 300

 -1

 0

 1

 0


А2

 3

 75

 0

 1

 1/2

 -1/2
II

 А1

 2

 75

 1

 0

 -1/2

 3/2
f(x)

 375

 0

 0

 1/2

 3/2


В симплекс-таблице II получен оптимальный опорный план,  поскольку все симплекс-разности (оценки)
j. Оптимальные значения переменных равны: x1*=75,  x2* =75 (основные переменные), x3*  =0, x4*  =0 (дополнительные переменные). Максимальное значение целевой функции равно 375.

Таким образом, в рассмотренной выше задаче об оптимальном использовании ограниченных ресурсов, оптимальная производственная программа состоит в выпуске 75ед. изделий первого вида и 75ед. изделий второго вида. С этой программой связана максимальная выручка от реализации готовой продукции – 375 у.е.


Список литературы, имеющейся в библиотеке ВЗФЭИ.


 

1.      Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В.Федосеева. – М.: ЮНИТИ, 1999. – 391 с.

2.      Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде ЕХСЕL  / Практикум: Учебное пособие для вузов. - М.:ЗАО Финстатинформ, 2000.-136 с.

[1]

Примечание: Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

[2]

Относительные и абсолютные ссылки.   В зависимости от выполняемых задач в Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, или абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$2, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки — нет.

[3]

Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мыщь по ячейкам, чьи адреса следует ввести.



Технология решения задач линейного программирования с помощью Поиска решений в среде EXCEL.


Поиск решения - это надстройка EXCEL, которая позволяет решать оптимизационные задачи. Ecли, в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту над­стройку. Выберите команду СервисÞ

Надстройки и активизируйте надстройку Поиск решения. Если же этой надстройки нет в диалоговом окне Надстройки,

то вам необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ

и с по­мощью программы установки Excel (или Office) установить надстройку Поиск решения.

 После выбора команд Сервис Þ

Поиск решения появится диалоговое окно Поиск решения.

В диалоговом окне Поиск решения есть три основных параметра:

• Установить целевую ячейку

• Изменяя ячейки

• Ограничения

Сначала нужно заполнить поле Установить целевую ячейку. Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или же уста­новить конкретное значение.

Второй важный параметр средства Поиск решения — это параметр Изменяя ячейки. Изменяемые ячей­ки — это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в це­левой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек. К изменяемым ячейкам предъявляется два основных требования. Они не должны содержать формул, и изменение их значений должно отражаться на изменении резуль­тата в целевой ячейке. Другими словами, целевая ячейка зависима от изменяемых ячеек.

Третий параметр, который нужно вводить, для Поиска решения – это ограничения.

        Для решения задачи необходимо:

1)      Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).


2)      Ввести исходные данные.

3)      Ввести зависимость для целевой функции

4)      Ввести зависимости для ограничений.

Запустить Поиск решений.

5)      Назначение целевой функции (установить целевую ячейку).

6)      Ввод ограничений.

7)      Ввод параметров для решения ЗЛП.

Рассмотрим технологию решения используя условия   Задачи 1 (Задача о костюмах).

Намечается выпуск двух видов костюмов - мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм - 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Tребуется определить,  сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского - 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

Сформулируем экономико-математическую модель задачи.

Введем следующие обозначения: х1 - число женских костюмов;     x2 - число мужских костюмов.

Прибыль от реализации женских костюмов составляет 10х1, а от реализации мужских 20х2, т.е. необходимо максимизировать целевую функцию

f(x) = 10´

х1 + 20´  х2 -> max.

Ограничения задачи имеют вид:

      х1      +        х2 £ 150                  - ограничение по труду

2
 х1  + 0.5
 х2 £  240                 - ограничение по лавсану

       х1 + 3.5
 х2 £  350                - ограничение по шерсти

            х2 ³  60                  - ограничение по костюмам

            х1 ³ 0

Решение.

1. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).

 

Обозначьте через Х1, Х2  количество костюмов каждого типа. В нашей задаче оптимальные значения вектора Х =(Х1, Х2,) будут помещены в ячейках A2:B2, оптимальное значение целевой функции в ячейке C3.



2. Ввести исходные данные.

Введите исходные данные задачи, как показано на рис.1.



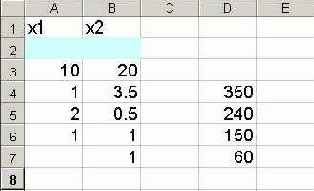
Рис. 1.

3. Ввести зависимость для целевой функции

 

•Курсор в ячейку «С3».

•Курсор на кнопку «Мастер функций», расположенную на панели инструментов.

•М1. На экране появляется диалоговое окно «Мастер функций шаг 1 из 2»

• Курсор в окно «Категория» на категорию «Математические».

• Курсор в окно «Функции» на «СУММПРОИЗВ» (рис.2)..

  



 

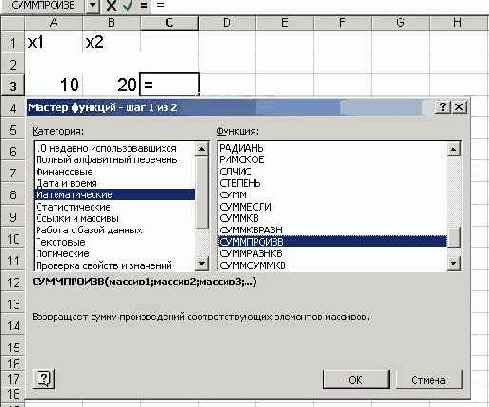
Рис 2.

На экране появляется диалоговое окно «СУММПРОИЗВ» (рис. 3)

 



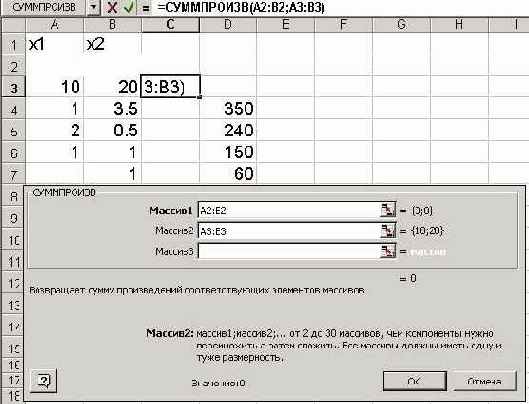
Рис. 3.

• В строку «Массив 1»[1]

ввести А2:В2

• В строку «Массив 2» ввести А3:В3.

 Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку[2].

 

На экране: в ячейку С3

введена функция (рис. 4).



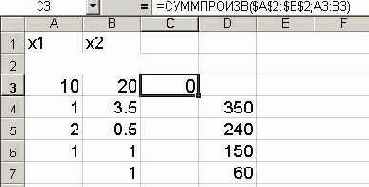
Рис. 4.

Ввести зависимости для ограничений.

• Курсор в ячейку «С3».

• На панели инструментов кнопка «Копировать в буфер».

• Курсор в ячейку «С4».

• На панели инструментов кнопка «Вставить из буфера».

• Курсор в ячейку «С5».

• На панели инструментов кнопка «Вставить из буфера».

• Курсор в ячейку «С6».

• На панели инструментов кнопка «Вставить из буфера».

• Курсор в ячейку «С7».

• На панели инструментов кнопка «Вставить из буфера».

 



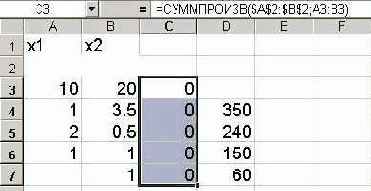
Рис.5.

Примечание. Содержимое ячеек С4 – С7 необходимо проверить. Они обязательно должны содержать информацию, как это показано для примера на рис.6 (в качестве примера представлено содержимое ячейки С5).



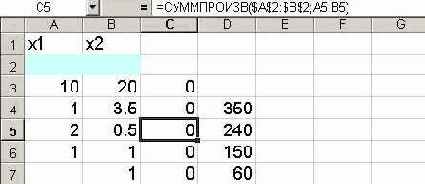
Рис. 6.

В строке «Меню» указатель мышки на имя «Сервис». В развернутом меню команда «Поиск решения». Появляется диалоговое окно «Поиск решения» (рис. 7).



 

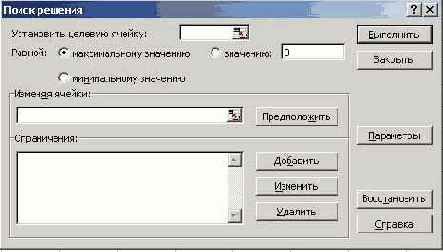
Рис. 7.

Назначить целевую функцию (установить целевую ячейку), указать адреса изменяемых ячеек.

 

• Курсор в строку «Установить целевую ячейку».

• Введите адрес ячейки «$С$3».

• Введите направление целевой функции в зависимости от условия вашей задачи: «Максимальному значению» («Минимальному значению»).



• Курсор в строку «Изменяя ячейки».

• Ввести адреса искомых переменных А$2:В$2. (Рис. 8.)



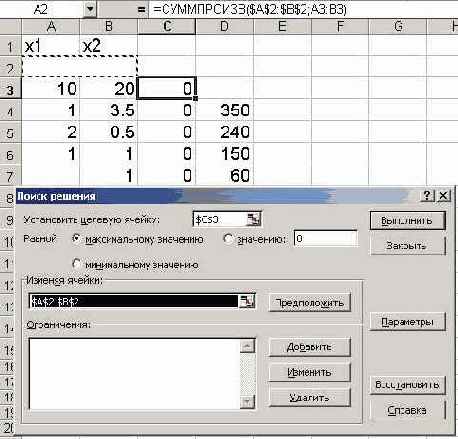
Рис. 8.

6. Ввести ограничения

• Указатель мышки на кнопку «Добавить. Появляется диалоговое окно «Добавление ограничения»

• В строке «Ссылка на ячейку» введите адрес $С$4.

• Ввести знак ограничения ?.

• В строке «Ограничение» введите адрес $D$4 (рис. 9)..

• Указатель мышки на кнопку «Добавить». На экране вновь диалоговое окно «Добавление ограничения».



• Введите остальные ограничения задачи, по выше описанному алгоритму

• После введения последнего ограничения кнопка «ОК».

На экране появится диалоговое окно «Поиск решения» с введенными условиями (рис.10).

.



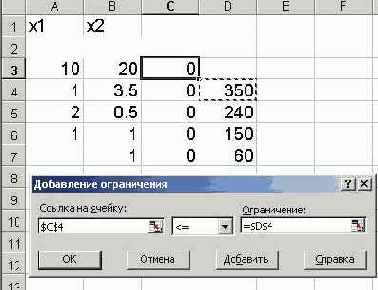
Рис. 9.

 



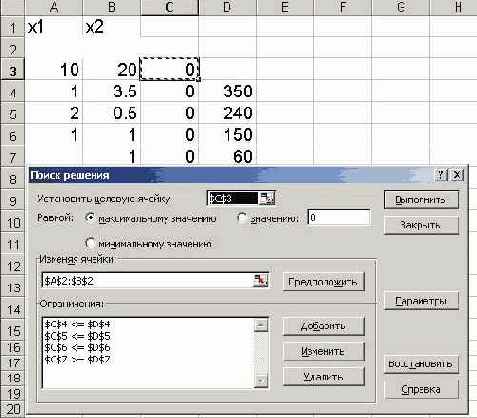
Рис.10

7. Ввести параметры для решения ЗЛП

 

• В диалоговом окне указатель мышки на кнопку «Параметры». На экране появляется диалоговое окно «Параметры поиска решения» (рис. 11).



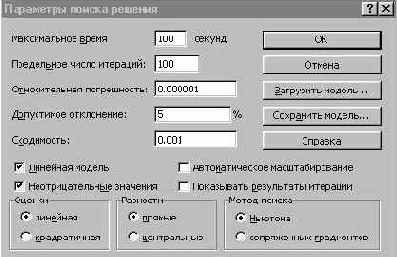
Рис.11

• Установите флажки в окнах «Линейная модель» (это обеспечит применение симплекс - метода) и «Неотрицательные значения».

• Указатель мышки на кнопку «ОК». На экране диалоговое окно «Поиск решения».

• Указатель мышки на кнопку «Выполнить».

Через непродолжительное время появится диалоговое окно «Результаты поиска решения» и

исходная таблица с заполненными ячейками А3:В3 для значений Хi и ячейка С3 с максимальным значением целевой функции (рис.12).



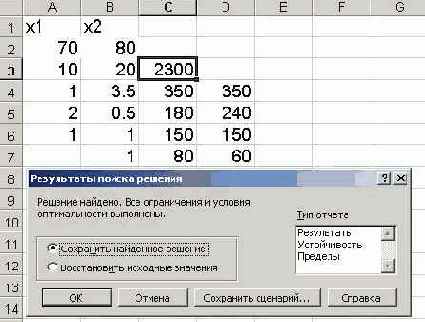
Рис.12

Если указать тип отчета «Устойчивость»,  то можно получить дополнительную информацию об оптимальном решении (Рис. 13).



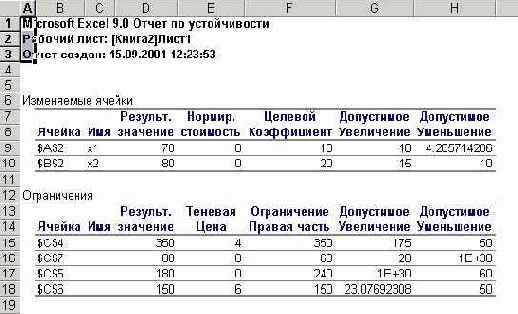
Рис. 13.

В результате решения задачи получили ответ:

Х1 = 70              -   необходимо сшить женских костюмов,

Х2 = 80              -   необходимо сшить мужских костюмов,

F(x) = 2300        что бы получить максимальную прибыль.

 

Решим еще одну задачу.

Задача 4.

(Задача о коврах)

Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т. п. Допустим, например, ресурсы трех видов рабочая сила, сырье и оборудование  имеются в количестве соответственно 80(чел/дней), 480(кг), 130(станко/часов). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса необходимых для производства одного ковра каждого вида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в табл.1.



                                                                                                                        Таблица 1

Ресурсы

 Нормы расхода ресурсов на единицу изделия

 Наличие

ресурсов
Ковер А

 Ковер В

 Ковер С

 Ковер D
Труд

 7

 2

 2

 6

 80
Сырье

 5

 8

 4

 3

 480
Оборудование

 2

 4

 1

 8

 130
Цена (тыс.руб.)

 3

 4

 3

 1
Требуется найти такой план выпуска продукции, при котором  общая стоимость продукции будет максимальная.

1. Сформулируем экономико - математическую модель задачи.

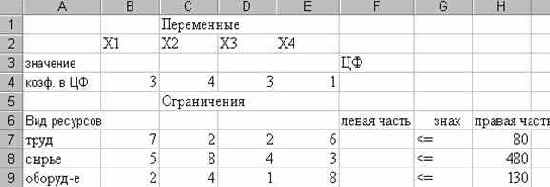
Обозначим через Х1,  Х2,  Х3,  Х4

количество ковров каждого типа.

Целевая функция  - это выражение, которое необходимо максимизировать  f(x) = 3Х1 +4Х2 +3Х3

+Х4

Ограничения по ресурсам

7Х1 +2Х2 +2Х3 +6Х4
80

5Х1 +8Х2 +4Х3 +3Х4
480

2Х1 +4Х2 +Х3 +8Х4
130

Х1, Х2, Х3, Х4
0

Решение

1. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).

 

Обозначьте через Х1, Х2, Хз, Х4 количество ковров каждого типа. В нашей задаче оптимальные значения вектора Х =(Х1, Х2, Хз, Х4) будут помещены в ячейках

ВЗ:ЕЗ, оптимальное значение целевой функции в ячейке F4.

2. Ввести исходные данные.

)Введем исходные данные в созданную форму. В результате получим (Рисунок 14):

Рисунок 14. Данные введены.

3 Введем зависимость для целевой функции

• Курсор в F4.

• Курсор на кнопку Мастер функций.

На экране диалоговое окно Мастер функций шаг 1 из 2.

• Курсор в окно Категория на категорию Математические.


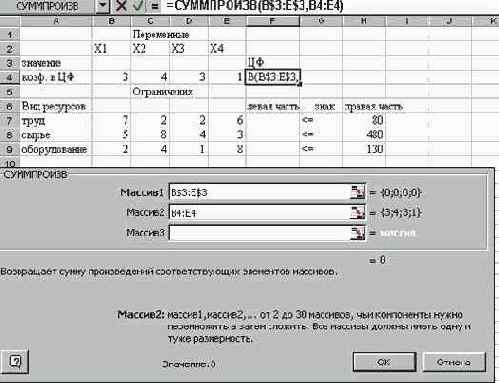
Рисунок 15.  Вводится функция для вычисления целевой функции.

• Курсор в окно Функции на СУММПРОИЗВ.                                                             

• В массив 1 ввести[3]

В$3:E$3.

• В массив 2 ввести В4:E4.

• Готово. На экране: в F4 введена функция, как показано на Рисунке 15.

4. Введем зависимость для левых частей ограничений:

• Курсор в F4.

• Копировать в буфер.

• Курсор в F7.

• Вставить из буфера.



• Курсор в F8.

• Вставить из буфера.                   

• Курсор в F9.

• Вставить из буфера.

На этом ввод зависимостей закончен.

Запуск Поиска решения.

6)      Назначение целевой функции (установить целевую ячейку).

¨      Курсор в поле Установить целевую ячейку.

¨      Ввести адрес $F$4.

¨      Ввести  направление целевой функции: Максимальному значению.

         Ввести адреса искомых переменных:

¨      Курсор в поле Изменяя ячейки.

¨      Ввести адреса В$3:E$3.

5. Ввод ограничений.

Курсор в поле  Добавить.

Появится диалоговое окно Добавление ограничения (Рисунок 16.).



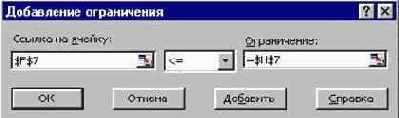
Рисунок 16. Ввод правых и левых частей ограничений.

· В окне Ссылка на ячейку ввести $F$7.

· Ввести знак ограничение  £..

· Курсор в правое окно.

·Вести $H$7.

· Добавить. На экране опять диалоговое окно Добавление ограничения. Ввести остальные ограничения.

· После ввода последнего ограничения  ввести ОК.

На  экране появится диалоговое окно Поиск решения с введенными условиями (Рисунок 17).



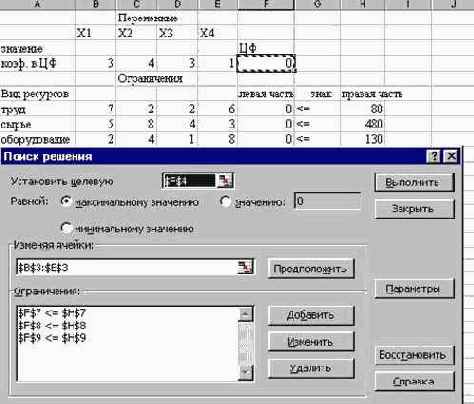
Рисунок 17. Введены все условия для решения задачи.

8) Ввод параметров для решения ЗЛП (Рисунок 18).

§         Открыть окно Параметры поиска решения.

§         Установить флажок Линейная модель, что  обеспечивает применение симплекс-метода.

§         Установить флажок Неотрицательные значения.

§         ОК (На экране диалоговое окно поиска решения).

§         Выполнить (На экране диалоговое окно результаты поиска решения – Рисунок 19.).



Рисунок 18. Ввод параметров.



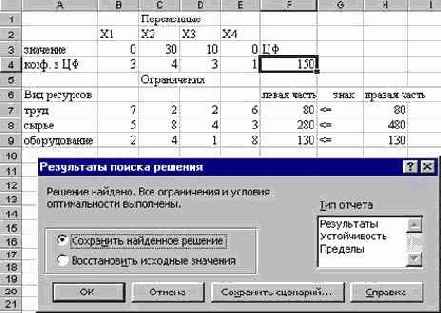
Рисунок 19. Решение найдено.

Полученное решение означает, что максимальный доход 150 тыс.  руб. фабрика может получить при выпуске 30 ковров второго вида и 10 ковров третьего вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 480 кг пряжи  (ресурс сырье) будет использовано 280 кг.



Создание отчета по результатам поиска решения

Excel позволяет представить результаты поиска решения в форме отчёта. Существует три типа таких отчетов:                                  

§         Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях

§         Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительно­сти решения к малым изменениям в изменяемых ячейках иди в формулах ограничений.                                  

§         Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние   границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

1. Отчет по результатам.

 Отчет по результатам
Целевая ячейка (Максимум)
Ячейка

 Имя

 Исходно

 Результат
$F$4

 коэф. в ЦФ ЦФ

 0

 150
Изменяемые ячейки
Ячейка

 Имя

 Исходно

 Результат
$B$3

 значение Х1

 0

 0
$C$3

 значение Х2

 0

 30
$D$3

 значение Х3

 0

 10
$E$3

 значение Х4

 0

 0
Ограничения
Ячейка

 Имя

 Значение

 Формула
$F$7

 труд левая часть

 80

 $F$7<=$H$7
$F$8

 сырье левая часть

 280

 $F$8<=$H$8
$F$9

 оборудование левая часть

 130

 $F$9<=$H$9
В  отчете по результатам  содержатся  оптимальные значения переменных Х1, Х2, Х3, Х4   , которые соответственно равны 0,10, 30,0;  значение целевой функции – 150,    а  также левые части ограничений.


и симплексным методом задачу линейного


1.
Решить графическим и симплексным методом задачу линейного программирования.
2.      Сформулировать двойственную задачу и найти ее оптимальный план, используя теоремы двойственности.
  Вариант 1
                 Max  f ( x ) = 3X1 + 2X2
                                           X1 + 2X2     ? 11
                                             2X1  -   X2   ?  5
                                               X1 + 3X2   ? 14
                                      X1 , X2   ? 0
Вариант 2
            Max  f ( x ) = 3X1 + 2X2
                      X1 + 2X2     ? 12
                     2X1  -   X2   ?  7
                       X1 + 3X2   ? 14
                       X1 , X2   ? 0
Вариант 3
Max  f ( x ) = 3X1 + 2X2
                   X1 + 2X2     ? 10
                 2X1  -   X2   ?  18
                   X1 + 3X2   ? 13
                     X1 , X2   ? 0
Вариант 4
            Min  f ( x ) = 3X1 + 2X2
                       X1 + 2X2     ?10
                      2X1  -   X2   ? 10
                        X1 + 3X2   ? 13
                         X1 , X2   ? 0
Вариант 5
Max  f ( x ) = 4х1+ 3х2
  х1 + 2х2   £ 10
  х1 + 2х2  ³ 2
2х1 +  х2  £ 10
 х1 ³
0,  х2 ³
0
Вариант 6
           Min  f ( x ) = 3X1 + 2X2
            X1 + 2X2     ?12
          2X1  -   X2   ? 12
             X1 + 3X2   ? 14
              X1 , X2   ? 0
Вариант 7
Max  f ( x )  = 3х1+ 5х2
 х1 + х2   £ 5
3х1   + 2 х2  £ 8
х1 ³
0,  х2 ³
0
Вариант 8
         Min  f ( x ) = 3X1 + 2X2
         X1 + 2X2     ? 11
       2X1  -   X2   ?  5
          X1 + 3X2   ? 14
          X1 , X2   ? 0
 
Вариант 9
Max  f ( x )    =  3х1+ х2
2х1 + 3х2 ³ 12
-х1 + х2 £
2
2х1 - х2 £
2
х1 ³
0,  х2 ³
0
Вариант 10
Max  f ( x )    =  3х1+ х2
х1 + х2 £
5
0.5х1 + х2 ³ 3
х1 - х2 ³
1
 

Используя Поиск решения, решить задачу


Используя Поиск решения, решить задачу оптимального использования ресурсов на максимум общей стоимости. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.
В каждой задаче требуется:
1.      Определить план выпуска продукции из условия максимиза­ции его стоимости.
2.      Определите ценность каждого ресурса (двойственные оценки) и его приори­тет при решении задачи увеличения запаса ресурсов.
3.      Определите суммарную стоимостную оценку ресурсов, ис­пользуемых при производстве единицы каждого изделия. Выпуск какой продукции нерентабелен?
4.      На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной про­дукции?
         Кроме того, в каждом варианте необходимо выполнить еще два пункта задания.
Вариант 1
         Для изготовления четырех видов продукции  используют  три  вида сырья. Запасы  сырья,  нормы  его  расхода и прибыль от реализации   каждого продукта приведены в таблице.

Тип
 Нормы расхода сырья на одно изделие
 Запасы
сырья
 А
 Б
 В
 Г
 сырья
I
 1
 2
 1
 0
 18
II
 1
 1
 2
 1
 30
III
 1
 3
 3
 2
 40
Цена изделия
 12
 7
 18
 10

5.      Определить, как изменятся общая стоимость продукции и  план ее выпуска при увеличении запасов сырья I и II вида на 4 и 3 единицы соответственно  и уменьшении на  3 единицы сырья III вида.
6.       Определить целесообразность включения в план изделия «Д» ценой 10 ед., на изготовление, которого расходуется по две единицы каждого вида сырья  ед.
Вариант 2
Для изготовления четырех видов продукции  используют  три  вида  сырья. Запасы  сырья,  нормы  его  расхода и прибыль от реализации  каждого продукта приведены в таблице.

Тип
 Нормы расхода сырья на одно изделие
 Запасы
сырья
 А
 Б
 В
 Г
 сырья
I
 1
 0
 2
 1
 180
II
 0
 1
 3
 2
 210
III
 4
 2
 0
 4
 800
Цена изделия
 9
 6
 4
 7
<
5.      Определить, как изменятся общая стоимость продукции и план выпуска  при увеличении запасов сырья II и III вида на 120 и 160 ед. соответственно и одновременном уменьшении на 60 ед. запасов сырья I вида;
6.      Определить целесообразность включения в план изделия «Д» ценой  12 ед., на изготовление которого расходуется по две единицы каждого вида сырья.
Вариант 3
Для изготовления трех видов продукции  используют  три  вида сырья. Запасы  сырья,  нормы  его  расхода и прибыль от реализации каждого продукта приведены в таблице.

Тип
 Нормы расхода сырья на одно изделие
 Запасы
Сырья
 А
 Б
 В
 сырья
I
 4
 2
 1
 180
II
 3
 1
 3
 210
III
 1
 2
 5
 244
Цена
 10
 14
 12

5.      Определить, как изменится общая прибыль продукции и план выпуска при увеличении запасов сырья I и III вида на 4 ед. каждого;
6.      Определить целесообразность включения в план изделия «Г», на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого   вида сырья  ценой 13 ед. и изделия «Д» на изготовление    которого расходуется по две единицы каждого вида сырья ценой 12 ед.
Вариант 4
Для изготовления четырех видов продукции  используют  три  вида  сырья. Запасы  сырья,  нормы  его  расхода и прибыль от реализации  каждого продукта приведены в таблице.

Тип
 Нормы расхода сырья на одно изделие
 Запасы
Сырья
 А
 Б
 В
 Г
 сырья
I
 2
 1
 3
 2
 200
II
 1
 2
 4
 8
 160
III
 2
 4
 1
 1
 170
Цена изделия
 5
 7
 3
 8

5.       Определить, как изменится общая стоимость продукции и план выпуска  при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно и одновременном уменьшении на 5 ед. запасов сырья III вида;


6.      Определить целесообразность включения в план изделия  «Д» на изготовление которого расходуется по две единицы каждого вида сырья и ожидается прибыль 10 ед.
  Вариант 5
На основании информации приведенной в таблице была решена задача оптимального использования ресурсов на максимум общей стоимости.

Ресурсы
 Нормы затрат ресурсов на единицу продукции
 Запасы
I
вид
 II
вид
 III
вид
Труд
 1
 4
 3
 200
Сырье
 1
 1
 2
 80
Оборудование
 1
 1
 2
 140
Цена
 40
 60
 80

5.      Определить, как изменится общая стоимость продукции и план выпуска  при увеличении запасов сырья на 18 единиц;.
6.      Определить целесообразность включения в план изделия четвертого вида на изготовление которого расходуется по две единицы каждого вида ресурсов  ценой 70 ед.
Вариант 6
На предприятии выпускается три вида изделий, используется при этом три вида сырья:

Сырье
 Нормы затрат ресурсов на единицу продукции
 Запасы
А
 Б
 В
 сырья
I
 18
 15
 12
 360
II
 6
 4
 8
 192
III
 5
 3
 3
 180
Цена
 9
 10
 16

5.      Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 45 кг., а II - уменьшить на 9кг.? 
6.     Целесообразно ли выпускать изделие Г ценой 11 единиц, если нормы затрат сырья 9, 4 и 6
кг.?
Вариант 7
Для изготовления трех видов продукции  используют четыре вида ресурсов. Запасы ресурсов,  нормы расхода и  цена каждого продукта приведены в таблице.

Ресурсы
 Нормы затрат ресурсов на единицу продукции
 Запасы
I
вид
 II
вид
 III
вид
Труд
 3
 6
 4
 2000
Сырье 1
 20
 15
 20
 15000
Сырье 2
 10
 15
 20
 7400
Оборудование
 0
 3
 5
 1500
Цена
 6
 10
 9
<


5.      Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 24? 
6.      Целесообразно ли выпускать изделие четвертого вида ценой 11 единиц, если нормы затрат ресурсов  8, 4, 20  и 6 единиц.?
Вариант 8
Предприятие выпускает 4 вида продукции и использует 3 типа основного оборудования: токарное, фрезерное, шлифовальное. Затраты на изготовление единицы продукции приведены в таблице; там же указан общий фонд рабочего времени, а также цена изделия каждого вида. 

Тип
 Нормы расхода сырья на одно изделие
 Общий фонд
оборудования
 А
 Б
 В
 Г
 раб. времени
 Токарное
 2
 1
 1
 3
 300
Фрезерное
 1
 0
 2
 1
 70
Шлифовальное
 1
 2
 1
 0
 340
Цена изделия
 8
 3
 2
 1

5.      Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если фонд времени шлифовального оборудования увеличить на 24 часа ? 
6.      Целесообразно ли выпускать изделие «Д» ценой 11 единиц, если нормы затрат оборудования 8, 2  и 2 ед.?
Вариант 9
На предприятии выпускается три вида изделий, используется при этом три вида сырья:

Сырье
 Нормы затрат ресурсов на единицу продукции
 Запасы
А
 Б
 В
 сырья
I
 1
 2
 1
 430 кг
II
 3
 0
 2
 460 кг
III
 1
 4
 0
 420 кг
Цена
 3
 2
 5

5.      Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 80 кг., а II - уменьшить на 10кг.? 
6.      Целесообразно ли выпускать изделие Г ценой 7 единиц, если нормы затрат сырья 2, 4 и 3 кг.?
Вариант 10
Для изготовления четырех видов продукции  используют  три  вида  сырья. Запасы  сырья,  нормы  его  расхода и прибыль от реализации  каждого продукта приведены в таблице.

Тип
 Нормы расхода сырья на одно изделие
 Запасы
Сырья
 А
 Б
 В
 Г
 сырья
I
 2
 1
 0,5
 4
 2400
II
 1
 5
 3
 0
 1200
III
 3
 0
 6
 1
 3000
Цена изделия
 7,5
 3
 6
 12

                  
5.      Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 100 кг, а II - уменьшить на 150кг.? 
6.      Целесообразно ли выпускать изделие «Д» ценой 10 единиц, если нормы затрат сырья 2, 4 и 3 кг?

Задания к контрольной работе


Номер Вашего варианта соответствует последней цифре  зачетной книжки.