БЛОК 1: Рост стоимости вложений за счет присоединения процентов

РОСТ СТОИМОСТИ ВЛОЖЕНИЙ ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ

При изучении этого блока вы узнаете, что такое:

процентная и учетная ставка;

обыкновенные и точные проценты;

простые и сложные проценты;

дискретные и непрерывные проценты;

номинальная, эффективная и реальная доходность.

При изложении материала далее используются следующие термины и обозначения:

Процентные деньги (англ. interest money), называемые часто коротко "проценты", представляют собой абсолютный доход от предоставления долга. Этот доход принято исчислять в сотых долях от размера вложенной суммы, то есть в процентах (от лат. pro centum – за сто).

PV – текущая стоимость (англ. present value) – исходная сумма долга или оценка современной величины денежной суммы, поступление которой ожидается в будущем, в пересчете на более ранний момент времени.

FV – будущая стоимость (англ. future value) – сумма долга с начисленными процентами в конце срока.

R – ставка процента (англ. rate of interest) является относительным показателем эффективности вложений (норма доходности), характеризующим темп прироста стоимости за период.

N – срок

погашения долга (англ. number of periods) – интервал времени, по истечении которого сумму долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов – обычно равных по длине подынтервалов времени, в конце которых регулярно начисляются проценты.

Процентная ставка R = (FV – PV) / PV измеряет уровень доходности отнесением абсолютного эффекта (полученного дохода в виде суммы процентных денег, начисленных за весь срок) к исходной сумме долгового обязательства PV. Интересно, что до социалистической революции в России слово "интерес" употреблялось как финансовый термин для обозначения суммы процентного дохода.

Если соотнести сумму процентов (FV – PV) не с PV, а с будущей стоимостью FV, наращенной по мере присоединения процентов, то получится другая мера эффективности – темп снижения                 D = (FV – PV) / FV, называемый в финансах учетной ставкой (англ. discount rate), или нормой банковского дисконтирования. Дисконтом в данном случае называется скидка в цене при продаже долгового обязательства (ценной бумаги) ниже номинала.

Задание Выразите процентную ставку R через учетную ставку D, используя соотношение R =

<
Пример. Вы заняли сегодня 4 руб., дав обязательство вернуть к указанной дате 5 руб.

Оценим доходность этой сделки для кредитора показателями нормы процента R и учетной ставки D, приняв весь период между двумя моментами времени за полный срок договора, приняв его за единицу времени N=1.

PV = 4 руб., FV = 5 руб., FV – PV = 5 – 4 = 1 руб., R = 1/4 = 25%, D = 1/5 = 20%.

Пример. Банк привлек денежные средства клиента в сумме 376 000 руб., в обмен на вексель (долговое обязательство) по предъявлении номиналом 509 500 руб., который через 6 дней был погашен.

Процентный доход клиента за 6 дней составляет 509 500 – 376 000 = 133 500 руб.

Процентная ставка за 6 дней 133 500 / 376 000 = 35,51%. За 1 день 35,51% / 6 = 5,9%.

Учетная ставка за 6 дней 133 500 / 509 500 = 26,20%. За 1 день 26,20% / 6 = 4,4%.

Простые проценты начисляются по ставке R на одну и ту же постоянную базу - исходную сумму долга PV, что за счет многократного прибавления постоянной величины процентного дохода за один период приводит к росту за полный срок N

периодов по закону арифметической прогрессии.



Множитель наращения по правилу простых процентов равен . Он показывает будущую стоимость одной денежной единицы, вложенной сроком на N периодов при начислении в конце каждого из них процентного дохода по ставке R без капитализации начисленных ранее процентов.

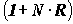
Таблица 1

Наращение и изъятие дохода при начислении простых процентов

Год	Сумма вклада в начале года (руб.)	Будущая стоимость (сумма на счете в конце года) при по ставке R = 15% годовых (руб.)	Процентный доход (снят со счета в конце года) (руб.)	Остаток на счете (руб.)
1	10 000	11 500 = (1+0,15)	1 500	10 000
2	10 000	11 500 = (1+0,15)	1 500	10 000
3	10 000	11 500 = (1+0,15)	1 500	10 000

Номинальные процентные ставки традиционно объявляются на период, равный одному календарному году N = 1, а срок более короткой финансовой операции измеряется обыкновенной дробью – долей года , 0 < N



< 1, которую получают как отношение срока операции t к длине целого года. Если учитывается точное число дней в году (T=365 или 366), то говорят о начислении точных процентов. При расчете обыкновенных процентов

год округляется до 360 = 12 месяцев по 30 дней. Срок операции t можно рассматривать точно или приблизительно.

Пример. Денежные средства в сумме 20 тыс.руб. приняты Банком в срочный вклад на 3 месяца.

Найдем будущую стоимость вклада при начислении процентов по ставке R = 29% годовых.

обыкновенные проценты с приближенным числом дней

тыс. руб.

обыкновенные проценты с точным числом дней

тыс. руб.

точные проценты с точным числом дней

тыс. руб.

Для точного расчета срока финансовой операции необходимо знать порядковые номера всех дней в году. Тогда срок t

находится как разность номеров дней заключения и окончания договора (в расчет процентов по вкладам добавляется еще один день, то есть полностью включаются все дни срока). Например, если долг образовался сегодня, а погашаться будет завтра, то следующие друг за другом даты отличаются на 1, а срок долгового обязательства, используемый при начислении процентов, при включении в него дат начала и окончания договора составляет 2 дня. При докомпьютерной технологии организации расчетов для ускорения вычислений используют справочную таблицу, подобную табл. 2.

Таблица 2

Порядковые номера дней в невисокосном году

Месяц число	1	2	3	4	5	6	7	8	9	10	11	12
1	1	32	60	91	121	152	182	213	244	274	305	335
2	2	33	61	92	122	153	183	214	245	275	306	336
3	3	34	62	93	123	154	184	215	246	276	307	337
4	4	35	63	94	124	155	185	216	247	277	308	338
5	5	36	64	95	125	156	186	217	248	278	309	339
6	6	37	65	96	126	157	187	218	249	279	310	340
7	7	38	66	97	127	158	188	219	250	280	311	341
8	8	39	67	98	128	159	189	220	251	281	312	342
9	9	40	68	99	129	160	190	221	252	282	313	343
10	10	41	69	100	130	161	191	222	253	283	314	344
11	11	42	70	101	131	162	192	223	254	284	315	345
12	12	43	71	102	132	163	193	224	255	285	316	346
13	13	44	72	103	133	164	194	225	256	286	317	347
14	14	45	73	104	134	165	195	226	257	287	318	348
15	15	46	74	105	135	166	196	227	258	288	319	349
16	16	47	75	106	136	167	197	228	259	289	320	350
17	17	48	76	107	137	168	198	229	260	290	321	351
18	18	49	77	108	138	169	199	230	261	291	322	352
19	19	50	78	109	139	170	200	231	262	292	323	353
20	20	51	79	110	140	171	201	232	263	293	324	354
21	21	52	80	111	141	172	202	233	264	294	325	355
22	22	53	81	112	142	173	203	234	265	295	326	356
23	23	54	82	113	143	174	204	235	266	296	327	357
24	24	55	83	114	144	175	205	236	267	297	328	358
25	25	56	84	115	145	176	206	237	268	298	329	359
26	26	57	85	116	146	177	207	238	269	299	330	360
27	27	58	86	117	147	178	208	239	270	300	331	361
28	28	59	87	118	148	179	209	240	271	301	332	362
29	29		88	119	149	180	210	241	272	302	333	363
30	30		89	120	150	181	211	242	273	303	334	364
31	31		90		151		212	243		304		365

<


Пример. Вы заняли 21 февраля 40 тыс.руб., обязавшись вернуть 23 августа сумму долга с точными простыми процентами по ставке 50% годовых.

По табл. 2 определяем номера дней. 21 февраля – это 52 день года, а 23 августа – 235 по счету день, если год невисокосный. Тогда t = (235 – 52) + 1 = 183 + 1 = 184 дня. 23 августа следует вернуть кредитору сумму тыс. руб.

Пример. 27 сентября 2000 года молодая семья разместила временно свободные денежные средства в сумме 40 тыс. руб. во вклад сроком 120 дней по ставке 9% годовых (см. табл. 3), предпочтя этот вариант двум индивидуальным вкладам по 20 тыс. руб. каждый.

Когда заканчивается срок вклада? Дата 27 сентября внутри года имеет порядковый номер 270. До конца года пройдет (365 – 270) + 1 = 96 дней. В 2001 г. вклад пролежит в Банке 120 – 96 = 24 дня. 24 января можно снять сумму срочного вклада с процентами. До момента явки вкладчика за деньгами средства переводятся на счет до востребования.

Множитель наращения по ставке 8% =

Множитель наращения по ставке 9% =

Выигрыш от инвестирования 40 тыс. руб. по более высокой ставке = = 131 руб. 51 коп.

Увеличение процентной ставки при удлинении срока депозита связано с тем, что, доверяя Банку свои сбережения на длительное время, клиенты ожидают получить компенсацию за повышение риска невозврата долга за счет повышения доходности сделки. Графическое представление зависимости доходности вложений от их срока принять называть "кривой доходности"3. Форма кривых доходности, построенных на рис.1 по данным табл. 3 о ставках вкладов в сумме свыше 30 тыс. руб. с начислением процентов в конце срока указывает на то, что в данном случае, привлекая средства на более длительное время, Банк меньше платит за риск, связанный со сроком, чем по более коротким депозитам.

Таблица 3

Ставки по вкладам физических лиц в рублях в Банке "Санкт-Петербург", % годовых

Срок	Порядок начисления процентов	20 марта 2000 года	25 сентября 2000 года
От 15 до 30 тыс. руб.	Свыше 30 тыс. руб.	От 15 до 30 тыс. руб.	Свыше 30 тыс. руб.
31 день	в конце срока	10,0	11,0	4,5	5,0
60 дней	в конце срока	18,0	20,0	5,5	6,0
91 день	ежемесячно	20,5	21,5	7,4	7,9
91 день	в конце срока	21,0	22,0	7,5	8,0
120 дней	ежемесячно	22,0	23,0	7,9	8,9
120 дней	в конце срока	23,0	24,0	8,0	9,0

<




Рис. 1. Кривая доходности.

Пример. Иван Спиридонович сделал 3 августа 1999 г. депозитный вклад в сумме 50 тыс. руб. на срок 365 дней по ставке 36% годовых, а Василий Семенович, ожидая роста процентных ставок по вкладам физических лиц в коммерческих банках, разместил такую же сумму на срок 120 дней, и затем дважды оформлял через 120 дней новый вклад, реинвестируя полностью исходную денежную сумму вместе с начисленными за 4 месяца процентами.

Используя табл. 2, определите дату окончания срока последнего (третьего) вклада Василия Семеновича на 120 дней?

Иван Спиридонович 3 августа 2000 г. может получить 50 тыс. руб., так как снижение Банком процентных ставок не распространяется на ранее заключенные срочные договора. Решение Василия Семёновича привело к такому финансовому результату (см. табл. 4).

Таблица 4

Реинвестирование вклада под простые проценты

Дата	Процентная ставка	Множитель наращения	Будущая стоимость
03/08/99	34%	1,11333	55,667
01/12/99	32%	1,23209	61,604
30/03/00	24%	1,33066	66,533

В данном случае за 360 дней средняя процентная ставка как годовой темп прироста в данном случае составила (66,533 – 50,000) / 50,000 = 33% годовых.

Ожидаемая вкладчиком выгода реинвестирования процентного дохода не была получена как в результате изменения условий приема вкладов, так и за счет более низкой ставки привлечения средств Банком на короткий срок.

Задание Оцените результат реинвестирования в условиях данного примера при сохранении процентной ставки по вкладам сроком на 120 дней на постоянном уровне R = 120% годовых.

Реинвестирование процентного дохода по постоянной ставке R является ступенчатым приближением к показательному росту по правилу сложных процентов , где буквой M обозначено число моментов реинвестирования.

При заключении между должником и кредитором финансового договора на срок, превышающий один расчетный период (N > 1) выбор базы для дальнейшего начисления процентов имеет принципиальное значение. Применение постоянной ставки начисления к постоянной базе дает рост по правилу простых процентов – арифметическую прогрессию с постоянной разностью, равной процентному доходу за период.



В краткосрочных операциях на срок до года (N

< 1) чаще используется правило простых процентов.

Сложные проценты характеризуются тем, что база начисления растет в результате регулярного присоединения к ней процентных денег, причитающихся кредитору за предыдущие расчетные периоды. Получается геометрическая прогрессия с постоянным знаменателем, равным множителю наращения (1 + R) за один период по ставке процентов R.



Таблица 5

Наращение и присоединение дохода при начислении сложных процентов

Год	Сумма вклада в начале года (руб.)	Будущая стоимость (сумма в конце года) при по ставке R = 15% годовых (руб.)	Процентный доход (присоединен к сумме вклада в конце года) (руб.)	Остаток на счете (руб.)
1	10 000	11 500 =	1 500	11 500
2	11 500	13 225 =	1 725	13 225.
3	13 225	15 209 =	1 984	15 209

Множитель наращения сложных процентов за полный срок N периодов по процентной ставке R за каждый является основным финансовым коэффициентом и показывает будущую стоимость 1 денежной единицы, вложенной на N периодов под сложные проценты, начисляемые в по ставке R.

Для обозначения данного финансового коэффициента используется стандартная аббревиатура FVIF (от англ. Future Value Interest Factor – процентный множитель будущей стоимости). Будущая стоимость определяется умножением размера первоначально инвестированной суммы на этот коэффициент

.



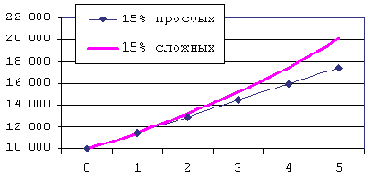
Рис. 2. Рост при начислении простых и сложных процентов по одинаковой ставке R.

Геометрический рост по правилу сложных процентов при N > 1 обгоняет арифметическую прогрессию простых процентов. Так, трижды заработав на вложенные 10 тыс. руб. проценты по 1,5 тыс. руб. в год, вкладчик имеет в конце срока = 14,5 тыс. руб., тогда как а наращение сложными процентами приносит ему будущую стоимость 15,209 тыс. руб. При удлинении срока вклада эта тенденция усиливается (см. рис. 2).

Задание По какой ставке простых процентов можно за 4 года нарастить сумму, равную будущей стоимости исходной суммы средств за тот же срок при начислении дохода по ставке 15% сложных годовых?

<


Для того, чтобы найти ответ необходимо выразить искомую ставку простых процентов R из условия равенства множителей наращения по простым и сложным процентам:

сложные проценты простые проценты



Пример. За два расчетных периода при начислении сложных процентов вклад вырос с PV = 75 руб. до FV2 = 112,5 руб.

Из формулы сложных процентов выразим ставку R.

.

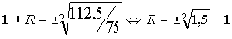
В качестве процентной ставки выбирается тот из двух возможных ответов данной математической задачи, который больше нуля. Так как результатам извлечения корня является иррациональное число (бесконечная дробь), ответ округляется с приемлемой точностью, например, до сотых R = 22,47%.



Рис. 3. Зависимость процентной ставки от срока наращения.

По этой ставке за два периода вклад вырастает в полтора раза. Общий вид зависимости ставки сложных процентов R от срока N при фиксированном значении коэффициента наращения и 2,0 представлен далее на рис. 3. Верхняя кривая соответствует большему значению FVIF(R; N) = 2.

Задание За какой срок (число процентных периодов) вклад удвоится при начислении простых процентов по ставке R = 30%? Множитель наращения простых процентов откуда За какой срок вклад удвоится при начислении сложных процентов по той же ставке? Отметьте соответствующую точку на рис. 3.

При более частом, чем один раз в год, начислении сложных процентов внутри года, размер номинальной годовой ставки R пропорционально уменьшают (традиция приближенных вычислений восходит к правилу простых процентов), а длину срока в процентных периодах увеличивают во столько же раз. Обозначим внутригодовую частоту начисления сложных процентов буквой m.

В случае ежемесячной капитализации (m

= 12) календарный срок 2 года выражается числом расчетных периодов периодов месяца, а ежемесячная процентная ставка получается из номинальной годовой делением на 12. Ясно, что при одинаковой номинальной годовой ставке R увеличение частоты начисления сложных процентов m приводит в конце каждого года к большему финансовому результату в виде будущей стоимости FV.



Через N полных лет

Эффективным годовым процентом называется процентный доход, получаемый инвестором за один год в результате вложения одной денежной единицы по номинальной годовой ставке сложных процентов R при частоте начисления m раз в год.

.

Абсолютная величина эффективного процента, отнесенная к одной целой денежной единице, дает годовую эффективную норму процента.

Эффективная доходность вложений является инструментом приведения условий финансовых контрактов к сопоставимому виду.

Задание У Вас есть свободная сумма PV = 1000 руб., которую Вы намерены пустить в рост на 12 месяцев под сложные проценты. Куда вы положите свои деньги, если доступные альтернативы таковы: Банк "Алиса" принимает вклады от населения под 16% годовых, начисляемых ежеквартально. Банк "Базилио" предлагает 12% годовых при ежемесячном начислении. Отделение иностранного банка "Carabas" дает 20% годовых, выплачиваемых каждые полгода.

Таблица 6

Сравнение условий приема вкладов по эффективной норме процента

Банк A ("Алиса")	Банк B ("Базилио")	Банк C ("Carabas")
16%	12%	20%	R – номинальная годовая ставка сложных %
4	12	2	m – частота внутригодового начисления %;
4% за квартал	1% в месяц	10% за полгода	ставка %, соответствующая длине внутригодового периода начисления
1,044 =	1,0112 =	1,12 =	FV – будущая стоимость вклада через 1 год (N = 1)

В современных условиях в связи с развитием систем электронных платежей проценты могут начисляться даже чаще, чем один раз в день. При бесконечно частом () дроблении года на малые процентные периоды, то есть при непрерывном наращении сложных процентов получается показательный закон роста , так как

при

Номинальную годовую процентную ставку R, являющуюся показателем степени в формуле множителя непрерывного наращения, называют интенсивностью, или силой роста. Она связана с годовой эффективной нормой процента соотношением . Будущая стоимость после непрерывного начисления сложных процентов за N лет





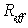
Конечный случай называют дискретным начислением процентов.

На реальную доходность вложений существенно влияет изменение покупательной способности денег за период, охватываемый финансовой операций. Процесс падения покупательной способности бумажных денег вследствие дополнительной эмиссии или по причине сокращении товарной массы при сохранении неизменного количества денег в обращении называется инфляцией

(от лат. influtio – вздутие). Инфляция проявляется в повышении стоимости жизни и росте цен.



Рис. 4. Сравнительная динамика индекса цен и валютного курса в 2000 г.4

Одним из подходов к измерению реальной покупательной способности фиксированной денежной суммы по прошествии срока N

является соотнесение ее с уровнем инфляции за N периодов. В каждом последующем инфляционном периоде обесцениваются уже ранее обесцененные деньги, поэтому реальная величина будущей стоимости, независимо от правила начисления процентов, применяемого для ее наращения, находится делением на цепной темп роста . С учетом инфляции реальная эффективная доходность I определяется по эффективной годовой ставке R и уровню инфляции h из условия

как

и в странах с низкой инфляцией знаменатель этой дроби в расчетах принимают иногда равным единице.

Уровнем инфляции h называется темп прироста индекса цен5 за выбранный период. Другим методом измерения инфляции, широко использовавшимся в России до 2000 г, является учет колебаний валютного курса (покупательная способность на один товар – иностранную валюту). Как видно выше на рис.4, к концу 2000 г. индекс потребительских цен заметно обогнал курс доллара США, который был стабилизирован и перестал быть индикатором инфляции.

Задание Какой реальный доход получит вкладчик, разместивший на срок на 1 год сумму 1000 руб. на условиях ежемесячного начисления сложных процентов по номинальной годовой ставке 17% и среднегодовом уровне инфляции 18%? Начните выполнение задания с расчета эффективного годового процента.

 

Пример. Располагая свободной на полгода суммой 1000 долл. США, предприниматель решил вложить их на срочный вклад и собрал информацию о ставках привлечения Банком на этот срок средств физических лиц в зависимости от вида валюты (см. табл. 7) с начислением простых процентов.



Таблица 7

Депозитные ставки и курсы обмена валют в начале и в конце срока договора

	RUR	USD	DEM
01/12/99 Сумма вклада	26 530	1 000
Обменный курс ЦБ РФ к рублю 01/12/99		26,53	13,66
Депозитная ставка на 180 дней, % годовых	31%	4%	3,5%
29/05/00 Будущая стоимость	30 642	1 020
Обменный курс ЦБ РФ к рублю 01/12/99	1 084	28,27	13,19
Депозитная ставка на 180 дней, % годовых	24%	3%	2,5%

Ожидая укрепления доллара США (не имея достоверного прогноза на 180 дней вперед), вкладчик предпочел внести средства на валютный депозит. Однако, если бы он конвертировал иностранную валюту и оформил свой вклад в российских рублях, результат наращения был бы выше:

.

Задание Оцените величину упущенного инвестором дохода в случае размещения той же суммы на валютный депозит через конверсию в немецкие марки. Каков эффективный годовой процент по этим валютным вкладам при полугодовом реинвестировании?

3 См.: Четыркин Е.М. Методы финансовых и коммерческих расчетов. М., 1995.

4 Источник: Госкомстат РФ – www.gks.ru

5 Пример расчета индекса цен на корзину продуктов см. далее в блоке 2.

 

БЛОК 2: Расчеты на персональном компьютере в электронной таблице Excel

Расчеты на персональном компьютере в электронной таблице EXCEL

Проработав материал этого блока в электронных таблицах на компьютере, вы научитесь:

вводить исходные данные в таблицу;

редактировать и форматировать табличные данные;

вводить расчетные формулы и копировать их;

применять абсолютные ссылки в формулах;

использовать встроенные функции;

подгонять данные под ответ;

по таблице числовых значений строить диаграммы.

При запуске программы Excel пользователю обычно предлагается для заполнения данными новый пустой документ в оперативной памяти компьютера со стандартным именем Книга1(Book1), состоящий из 16 рабочих листов, разграфленных в виде таблицы на 16384 строки и 256 столбцов, стандартная ширина каждой клетки равна 9 символам. Экран компьютера в начале стандартного сеанса работы программы выглядит как на рис. 4.

Рис. 4. Вид окна (программы (обработки)) электронных таблиц Excel при запуске.

Исходное положение указателя текущей клетки внутри видимой на экране части таблицы – пересечение первой строки и первого столбца, это клетка с адресом A1 в одноименном стиле ссылок.

Альтернативный стиль ссылок на ячейки рабочего листа, когда столбцы также нумеруются, а номер строки указывается в первую очередь, можно активизировать командой Сервис Параметры, выбрав в ее диалоговом окне на вкладке Общие в группе Стиль ссылок позицию переключателя i R1C1. Тогда первая клетка (ячейка) рабочего листа так и будет именоваться R1C1, от английского Row1Column1 (ряд первый, колонка первая).

Движение указателя по табличному полю рабочего листа необходимо для выбора заполняемых, редактируемых, форматируемых или просматриваемых пользователем ячеек. Выбранная указателем ячейка является тривиальным выделенным диапазоном. Выделение диапазона ячеек, с которыми необходимо произвести те или иные действия, предшествует выполнению большинства команд и задач.

Для выделения прямоугольного диапазона ячеек, сделайте текущей клеткой один из его будущих углов, поместите указатель мыши внутрь рамки выделения клетки (он должен иметь при этом форму толстого белого плюса), и удерживая нажатой левую кнопку мыши, перемещайте ее, при этом выделяемый блок клеток будет закрашиваться цветом, контрастным к основному фону таблицы. При освобождении нажатой кнопки мыши выделение блока заканчивается. Для отмены текущего выделения достаточно изменить положение указателя в таблице.

Непрерывное перемещение указателя в любом направлении инициируется мышью (выбор позиции фиксируется щелчком), а дискретное – стандартными управляющими клавишами, назначение большинства из которых дано в табл. 8.

Таблица 8

Основные клавиши управления положением табличного указателя текущей клетки

Направление		Шаг движения
на одну клетку	на один экран	до конца блока данных или границы рабочего листа
вниз	¯	PageDown	End,затем ¯
вверх	Ý	PageUp	End, затем Ý
направо	®	удерживая Ctrl, нажать ®	End, затем ®
налево	¬	удерживая Ctrl, нажать ¬	End, затем ¬

Кроме того, для прямого прыжка в клетку с явно заданным адресом используется клавиша F5, а клавиша Home активизирует первую ячейку той строки таблицы, где был указатель до ее нажатия.

Задание Сколько клеток помещается в таблице на одном рабочем листе стандартной книги Excel? 1) Переведите указатель до конца рабочего листа вниз и направо; 2) Для определения номера последнего столбца активизируйте стиль ссылок R1C1; 3) Перемножьте (расчетную формулу можно разместить в любой свободной клетке) номер последней строки на номер последнего столбца.

Переход на другие листы табличной книги достигается щелчком мыши по ярлычкам, либо парными комбинациями служебных клавиш: Ctrl+PageUp и/или Ctrl+PageDown. Переименование рабочего листа

инициируется двойным щелчком левой кнопки мыши по ярлычку, после чего можно вводить новое имя.

Задание Вызовите интерактивную справочную систему (пункт меню ? или клавиша F1), введите для поиска в Предметном указателе ключевую фразу "выделение ячеек", и, прочитав полученные инструкции, попрактикуйтесь в выделении небольших прямоугольных областей.

Для записи нового документа в виде файла электронной таблицы на диск используется команда Файл Сохранить как..., в диалоге с которой пользователь выбирает нужную папку на диске, а также имя и тип создаваемого файла. Для таблиц Microsoft Excel



по умолчанию предусмотрено расширение *.XLS

Теперь перейдем к изучению правил ввода данных, и начнем его с источника некоторых недоразумений, смущающих неподготовленных пользователей, желающих самостоятельно начать работу с табличным процессором Excel.

Пример. Предположим, что мы хотим организовать учет расходов домашнего хозяйства на приобретение фруктов и овощей.

Например, было куплено 850 г апельсинов по цене 12 руб. 56 коп. за 1 кг... Запишем в первую строку таблицы рабочего листа эту информацию. В столбец A будем вносить названия, в столбец B – вес покупки, а в столбец C – цену...



Рис. 5. Заполнение первой клетки таблицы данными примера 1 в режиме ввода с клавиатуры.

Данные вводятся на рабочий лист электронной таблицы порциями, обычно последовательно вводят информацию в несколько соседних ячеек, поочередно заполняя каждую из них. При нажатии пользователем алфавитно-цифровой клавиши текущая клетка таблицы автоматически переходит в режим ввода, готовясь принять данные, распознать их тип, хранить полученное значение и выводить его в заданном формате.

Для ввода данных необходимо:

сделать заполняемую клетку текущей (перевести туда рамку указателя);

набрать последовательность символов на клавиатуре, при этом вводимая строка в Excel отображается и в заполняемой клетке, и над полем таблицы в строке формул;

закончить ввод нажатием клавиши ввода ¿ Enter, либо щелчком мыши по заменяющей ее экранной кнопке с изображением зеленой галочки (символ a ), расположенной в режиме ввода над полем рабочего листа в левой части строки ввода.

В состоянии ввода данных, воспроизведенном на рис. 5, нужно добавить к набираемому слову еще одну букву, чтобы название фруктов стояло во множественном числе, и можно заканчивать ввод.

Для исправления допущенных при наборе опечаток после выхода из режима ввода можно

повторить ввод данных в ту же клетку;

отредактировать текущую клетку, дважды щелкнув по ней мышью, или нажав клавишу F2.

Отменить незаконченный ввод можно клавишей Esc, или экранной кнопкой с красным крестиком (символr ) в строке ввода.



Если данные набраны правильно, но введены ошибочно не в ту клетку, их можно перенести, например, методом перетаскивания: подведя снизу указатель мыши к рамке выделенной ячейки с данными (он должен принять форму толстой белой стрелки), нажать левую кнопку и, удерживая ее, перемещать манипулятор, ориентируясь на пунктирную рамку положения клетки, принимающей перенос.

Для полной очистки текущей клетки от ранее введенной информации нажимайте клавишу Delete.

После успешного заполнения боковика таблицы первой поясняющей надписью можно переходить ко вводу исходных числовых данных о весе и цене покупок. Посмотрим, как это получилось у начинающего пользователя, экран которого воспроизводится на рис. 6.

В России принято отделять целую часть дробного числа знаком запятой, а в США – десятичной точкой. В зависимости от состояния параметров настройки версии Windows на национальный стандарт страны использования компьютера, в Excel корректным разделителем в составе числа может оказаться либо точка, либо запятая, но они не могут свободно заменять друг друга и быть допустимыми символами-разделителями одновременно.



Рис. 6. Превращение числовой информации в календарную в результате ошибки кодирования.

Вы точно не ошибетесь в том, какой же символ

– точку или запятую можно использовать в десятичных дробях, если будете набирать числа не верхнем ряду основной часть клавиатуры, а на дополнительной, в режиме NumLock. Кроме / * - + 9 8 7 6 5 4 3 2 1 0 и клавиши ввода, там есть клавиша с изображением десятичной точки (совмещенная с Del). При работе в Excel она всегда вводит именно тот символ, который и следует использовать как разделитель при записи десятичного числа.

В нашем примере при вводе веса в килограммах пользователем правильно была поставлена запятая, а ввод в клетку C1 в качестве значения цены в рублях числа 12.56 (через точку) приводит к тому, что, благодаря действию настройки компьютера на точку как разделитель компонентов даты, эти пять символов интерпретируются программой как начало 12-го месяца 56-го года текущего века (сначала предпринимается попытка отыскать в календаре 56-й месяц). В строке формул это значение и показано – 01.12.1956, что соответствует 1 декабря, причем дата здесь выводится сокращенно, без указания номера года, как 1.12 в клетке C1.



В зависимости от текущей установки краткого формата даты, пользователь может увидеть и другие варианты, например запись без номера дня – дек.56

Если попробовать улучшить положение, преобразовав дату, появившуюся в результате неправильного ввода десятичного числа, к денежному формату, например, нажав соответствующую кнопку на панели инструментов (см. рис.6), то результатом таких усилий будет 20 790р., что в качестве цены килограмма апельсинов вместо исходного значения 12,56 р. выглядит несколько неожиданно.

Откуда же появилось это загадочное пятизначное число? Дело в том, что в Excel даты кодируются путем пересчета дней с начала века, в этой системе день номер 1 – это 1 января 1900 года. Сериальное число 20790 обозначает точное количество дней, прошедших между началом XX столетия и 1 декабря 1956 г. Рецептом исправления показанной на рис.6 ошибки является только повторный ввод числа 12,56 в ту же самую клетку C1, но теперь уже правильно – через запятую. Поскольку в процессе эксперимента этой клетке был назначен денежный формат с округлением до целых, то на экране появится цена 13р. без копеек.



Рис. 7. Увеличение точности округления при выводе значения десятичной дроби на экран.

Обратите внимание, что в строке формул (см. рис. 7) выводится истинное значение введенной в текущую клетку числовой константы 12,56. Для его вывода в денежном формате с точностью до копеек нужно совместить белую стрелку указателя мыши с экранной кнопкой Увеличить разрядность панели инструментов Форматирование и пару раз "нажать на нее", щелкая мышью. Тогда получится 12,56р.

В зависимости от состава вводимой информации, и особенно от её первого символа (префикса) данных электронные таблицы автоматически относят их после ввода к одному из двух типов: константа

или формула. Табличные формулы начинаются с префикса и могут состоять из:

числовых констант,

знаков действий и скобок,

адресов и/или имен табличных диапазонов и отдельных клеток,

имен встроенных функций.

Префиксами формулы, с которых обязательно начинается ее ввод, могут быть символы =, + и -



При вводе последовательности символов, которая ни с какого префикса формулы не начинается, данные интерпретируется программой как константа – число, дата или текст.

Числовое выражение может состоять только из цифр, знаков "плюс", "минус" круглых и фигурных скобок и некоторых других знаков, предусмотренных дробным, процентным, экспоненциальным, денежным и финансовым форматами.

Даты хранятся как целые числа, хотя формат их записи больше похож на текст.

Текстом являются любые данные, которые программе не удается распознать как число или формулу, в том числе и данные, подразумеваемые как числа и формулы, при вводе которых были допущены ошибки.

Текст при вводе выравнивается по левому краю ячейки, а даты, числа и формулы - по правому. Если формат вывода значения числового выражения (константы или результата формулы) не помещается на экране в ширину клетки, то вместо него для привлечения внимания пользователя выводится "заборчик" знаков нумерации #########. Если же в ширину столбца не укладывается текст, а ячейка справа по строке уже занята, то окончание длинного текста усекается.

Задание Продолжите ввод данных примера, ориентируясь на числовые значения и пояснения к выполнению операций, данные ниже на рис. 8.

Действия оператора по приведению в порядок вида таблицы после ввода данных: Увеличена ширина первого столбца. Вставлена новая первая строка. Текст в строке 1 выровнен по центру. Текст в A10 выровнен по правому краю. Увеличена до тысячных) разрядность записи веса апельсинов в клетке B2. Формат клеток B2 и C2 признан образцовым и скопирован вниз. Слова, напечатанные здесь полужирным шрифтом, являются ключевыми для Вашей самостоятельной работы с Предметным указателем Справочной системы Excel

Рис. 8. Заполнение таблицы исходными данными и их элементарное форматирование.

После заполнения блока таблицы информацией пора переходить к расчетам. Найдем, например общую сумму затрат. Организовать ее вычисление пользователь Excel может несколькими способами.



Самый традиционный подход – найти затраты на отдельные продукты (путем перемножения веса каждого продукта на цену), а затем сложить их вместе.

Чтобы узнать, сколько нужно заплатить за 850 г апельсинов при цене 12,56 р./кг, можно просто поместить в ячейку D2 формулу произведения числовых констант Этот способ соответствует использованию табличной клетки в качестве аналога калькулятора арифметических выражений, только клавиша = в Excel при наборе расчетного выражения нажимается первой, а не последней.

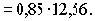
Современные калькуляторы, а тем более персональные компьютеры, хранят в своей памяти не только данные, но и алгоритмы решения задач, их можно программировать. Клетка рабочего листа электронной таблицы соответствует ячейке машинной памяти, предназначенную для хранения изменяемой в процессе работы информации, а имена клеток похожи на идентификаторы переменных в языке программирования и имеют то же назначение. Чтобы запрограммировать некоторое простое вычисление, нужно закодировать его расчетную формулу адресами клеток с исходными данными, соединенными знаками действий в корректное математическое выражение и ввести его в нужное место таблицы, например формулу =B2*C2 поместить в ячейку D2. Чтобы не промахнуться с координатами клеток и не наделать при буквенно-цифровом наборе опечаток, рекомендуется вставлять в формулы табличные адреса, просто щелкая мышью по клеткам с операндами (см. рис. 9). При этом клавишу = , скобки и знаки действий удобно нажимать свободной от мыши рукой.



Рис. 9. Ввод в таблицу формулы с указанием ссылок щелчком по клеткам

без нажатия алфавитных и цифровых клавиш для набора адресов сомножителей.

При использовании в записи формул табличных адресов сомножителей вместо их фиксированных числовых значений результат, конечно, не изменится, но при необходимости повторить расчет затрат, например, на покупку того же веса апельсинов при изменении цены на них, не потребуется еще раз полностью набирать оба сомножителя и знак действия, а достаточно только переправить одну цену в ячейке C2, и таблица автоматически отреагирует новыми значениями всех зависимых ячеек.



Исчислив расходы на апельсины – 10,68р., можно переходить к программированию аналогичных действий в следующей строке и далее вниз до конца списка продуктов. Только что введенная формула отражает суть расчетной модели, в каждой строке одинаковой – число из колонки B умножить на число из колонки C, а значение их произведения вывести на экран в колонке D.

а) выделение блока клеток, принимающих копию

б) освобождение левой кнопки мыши

Рис. 10. Процесс копирования формулы на блок клеток вниз движением мыши.

Для кодирования повторяющихся вычислений в электронных таблицах применяется технология копирования клеток с формулами.

Источником формулы в нашем примере будет клетка D2, а копировать ее нужно вниз по столбцу на блок ячеек D3:D9. После того как исходная формула правильно записана и введена в клетку-источник, которая уже является текущей, необходимо совместить указатель мыши с угловым манипулятором рамки выделения. Указатель, бывший до того толстым белым плюсом, станет более тонким черным крестом.

Удерживая нажатой левую кнопку при этом положении указателя, перемещайте мышь вниз, и границы блока принимающих копию ячеек будут постепенно выделяться на экране пунктиром (см. рис. 10а). Когда Вы освободите левую кнопку мыши, формула перемножения цены данного товара на количество распространится из блока-источника на весь выделенный диапазон ячеек с адаптацией используемых табличных ссылок в стиле "параллельного переноса" (см. рис. 10б).

Не торопитесь отменять выделение блока клеток, сохранившееся после окончания копирования, а нажмите в этом состоянии экранную кнопку Автосуммирование панели инструментов Стандартная (на кнопке изображен математический символ операции суммирования – большая греческая буква S , читается "сигма"), и под выделенным блоком в результате автоматической подстановки формулы =СУММ(D2:D9) в ячейке D10 возникнет значение самой популярной встроенной табличной функции, удостоенной персональной кнопки на стандартной панели инструментов. При копировании адреса клеток в составе формулы адаптируются к направлению копирования – в нашем случае номера строк будут расти с шагом 1 от строки к строке.



Копирование формулы на блок клеток – не единственный способ кодирования повторяющихся вычислений средствами современных электронных таблиц. Обработку набора однотипных элементов общей операцией в языках программирования оформляют оператором цикла. Счетчик цикла при этом перебирает подряд все номера элементов массива. Такая структура данных есть в Excel, но клетки собираются вместе в массив не явно по номерам, а выделением нужного блока мышью. Так, умножение веса на цену можно выразить формулой массива.



Рис. 11. Ввод формулы массива в выделенный диапазон.

Для ее ввода нужно выделить в таблице заполняемый блок клеток D2:D9, набрать расчетную формулу =B2:B9*C2:C9, и закончить ее ввод (не в одну клетку, а в весь выделенный блок) уже не привычным нажатием клавиши ввода, а комбинацией трех соседних клавиш Ctrl-Shift-Enter.

Такая формула заполняет сразу весь выделенный блок, и необходимость в копировании отпадает. Обратите внимание, что в строке ввода формула массива, которой подчинена текущая клетка, отображается в фигурных скобках {=B2:B9*C2:C9}.

Использование в таблице формул массива оправдывает трудоемкость их создания, если необходимо целиком подчинить блок клеток влиянию единой формулы и исключить возможность изолированного исправления содержимого отдельных клеток внутри массива (степень защиты).

Есть еще один способ расчета затрат, не требующий к явного вычисления в таблице отдельных частных слагаемых. С точки зрения экономиста-математика, затраты на приобретение набора товаров исчисляются как скалярное произведение векторов количества товаров и цен.

Пусть – количество продуктов (в нашем примере их семь);

– номер продукта в упорядоченном списке, меняется от 1 до ;

– приобретенное количество-го продукта;

– цена, по которой приобретается -ый продукт. Тогда затраты на приобретение содержимого данной фруктово-овощной корзины есть сумма покоординатных произведений элементов векторов и .



где – вектор, в элементах которого записан вес покупаемых продуктов;



– набор соответствующих цен.

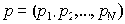
Столь широко распространенная в быту учетная операция уже закодирована в Excel встроенной математической функций. В оригинальной (англо-американской) версии пакета она называется =SUMPROD, а в русифицированной имеет идентификатор =СУММПРОИЗВ, что с точки зрения вводимой длины строки и вероятности опечатки при посимвольном наборе менее удачно.

Для избежания ошибок при вводе длинных формул рекомендуется выбирать название нужной функции из готового списка имен, раскрывающегося при обращении к процедуре Мастер функций. Она активизируется кнопкой со значком (см. рис. 12): на панели инструментов Стандартная.

Попробуем обратиться ко встроенной функции =СУММПРОИЗВ для помещения итоговой величины затрат в клетку D10. Для этого нужно выделить эту клетку D10 переводом в нее (рамки) табличного указателя, а затем щелкнуть по кнопке Мастер функций, либо использовать команду меню Вставка Функция...

На шаге 1 в левом окне выбирается Категория функций – Математические v , а затем в правом окне прокручивается алфавитный список имен всех встроенных функций выбранной категории.

На шаге 2 определяются аргументы выбранной функции. Аргументами функций могут быть константы, или табличные ссылки на хранящие их клетки. В нашем примере сошлемся на интервалы ячеек таблицы, куда были введены вес и цена каждого продукта, как отдельные элементы скалярно перемножаемых нами векторов.

Диалоговое окно Мастера функций обычно всплывает на экране как раз в таком положении, что закрывает собой нужные ячейки рабочего листа, но его легко подвинуть в сторону мышью, удерживая нажатием левой кнопки мыши стрелку экранного указателя на строке заголовка. Когда данные о весе станут целиком видны на экране, достаточно их выделить (клетки будут обводиться пунктиром), чтобы ссылка на соответствующий диапазон B2:B9 синхронно вписалась в поле ввода табличных координат первого аргумента функции. Затем точка ввода данных | щелчком мыши переводится вниз в поле ввода второго аргумента, и аналогично закрашиваются данные о ценах – C2:C9.





Рис. 12. Состояние ввода в текущую ячейку обращения к функции с помощью Мастера функций

Теперь можно закончить вызов функции, нажав на клавишу ввода или экранную кнопку Готово диалогового окна Мастера функций (крайняя справа внизу). В случае успеха в текущую клетку D10 нами введена последовательность символов =СУММПРОИЗВ(B2:B9;C2:C9), воспринимаемая программой Excel как расчетная формула, состоящая из только обращения к стандартной функции.

В клетке таблицы после ввода в нее формулы появляется ответ – в примере 1 это числовое значение 205,6795, а производящая формула видна над полем таблицы в строке ввода, если клетка выделена текущим положением рамки табличного указателя. Предлагаем читателю самостоятельно справиться с форматированием полученного значения, например вывести его в денежном стиле с точностью до копеек.

Предположим теперь, что вес купленных в условиях примера 6 бананов увеличился до 1,5 кг.

Если справиться с заменой значения в клетке B5 прямым вводом "сверху" нового числа, то после приема значения данных итог затрат мгновенно станет равен 216,27р., так как электронная таблица автоматически обновляет результаты формул при изменении исходных данных, значения которых заданы не константами, а табличными ссылками на другие клетки (ячейки).

Клетки, на которые ссылается формула текущей, называются зависимыми.

Клетки, формулы которых ссылаются на текущую, называются влияющими.



Рис. 13. Поиск на рабочем листе клеток таблицы, в которых есть формулы, зависящие от текущей.

При организации сложных вычислений в таблице важно следить за образующейся структурой формул. Неоценимую помощь в этом способна оказать панель инструментов Зависимости (см. рис. 13).

Задание При помощи средств панели инструментов Зависимости, выявите технологические различия между тремя использованными способами организации в таблице вычисления одной и той же суммы затрат

Предположим теперь, что мы направились за покупками, имея в кармане ровно 200 руб., и, как уже выяснилось, на приобретение всего содержимого отобранной корзины их не хватит. Не имея возможности изменить цены, подумаем, как можно уменьшить вес картофеля, чтобы уложиться в бюджетное ограничение.



Попробуем просто вводить в ячейку B8 новые числа – 3,5 (можно побольше), 4 (надо чуть поменьше), и так далее... Этот процесс подбора в Excel автоматизирован. Для вызова процедуры подбора значения одного параметра, приводящего цепочку формул к нужному ответу, дадим команду Сервис Подбор параметра...



Рис.14. Диалоговое окно процедуры численного решения неявных уравнений.

Процедура Подбор параметра позволяет (см. рис. 14) установить в зависимой ячейке (содержащей расчетную формулу) искомое числовое значение, изменяя значение влияющей (на значение зависимой от неё формулы) ячейки. С ее помощью пользователь Excel получает возможность находить решающее значение (корень) неявного уравнения, не прибегая к выводу явной аналитической зависимости

При этом левая часть уравнения может быть достаточно сложной и кодироваться даже не одной, а несколькими формулами, связанными между собой табличными ссылками (адресами клеток) в общую зависимость.

Заметим, что если решений несколько, то находится только одно из них – ближайшее к начальному значению влияющей ячейки, которое при подгоне к нужному ответу изменяется. Если нужно найти другой корень – повторите подбор с другим начальным приближением. Давайте подробнее изучим влияние частных затрат на приобретение каждого продукта на показатель "Затраты ИТОГО".

Нагляднейшей формой сравнения чисел является построение по таблице данных графиков стандартного типа с помощью процедуры Мастер диаграмм, которая активизируется кнопкой панели инструментов Стандартная, или через меню выбором командной последовательности Вставка Диаграмма...

При вставке диаграммы на тот же рабочий лист, где находятся исходные данные, необходимо указать щелчком по табличному полю будущее положение её левого верхнего угла, а затем ограничить размер окна диаграммы диагональным движением манипулятора правее вниз, удерживая нажатой левую кнопку до завершения выделения пунктиром требуемых границ окна.



Рис. 15. Выделение диапазона, содержащего данные для построения диаграммы –



шаг 1.

На шаге 2 выберем тип диаграммы – Круговая, а на шаге 3 – вид диаграммы (7).

Интересно, что процедурой Мастер диаграмм автоматически вычисляются при этом удельные доли затрат в общей сумме, ведь в таблице этих данных в явном виде просто нет. Давайте проверим расчет долей отдельных слагаемых в сумме затрат, повторив его с точностью большей, чем до целых процентов.

Удельный вес каждого слагаемого – дробь, в числителе которой стоит текущее слагаемое, а знаменатель всех – полная сумма числителей. Удельный вес затрат на апельсины рассчитывается по формуле =D2/D10. Если мы скопируем ее вниз, то получим =D3/D11, =D4/D12, ...

Как только ссылка знаменателя укажет на пустую клетку D11 (по умолчанию числовое её значение считается нулевым), произойдет вывод сообщения об ошибке: предпринимается попытка выполнить математически некорректную операцию – разделить положительный числитель на ноль (сообщение #ДЕЛ/0!).



Рис. 16. Круговая диаграмма по числовым значениям формул в диапазоне D2:D9



Рис. 17. Табличная модель вычисления частных долей общих затрат.

Чтобы закрепить в формуле знаменателя номер 10 строки, защитить его от изменения при копировании выражения вниз на другие строки, необходимо вставить перед 10 знак доллара $, после чего адрес клетки станет абсолютным и запись формулы примет вид =D2/D$10

Это исправление в режиме редактирования содержимого клетки можно сделать, переключившись на латинский алфавит, и нажав знак $ в верхнем ряду клавиатуры (этот символ совмещен с цифрой 4), причем одновременно придется удерживать Shift – клавишу переключения регистра.

Удобнее при редактировании превращать адрес клетки в абсолютный, нажимая клавишу F4. Тогда адрес D10, на который указывает точка ввода | , будет сам последовательно преображаться во все возможные варианты: абсолютный $D$10, смешанные D$10 и $D10, относительный D10.

При копировании формулы =D2/D$10 вниз получится последовательность выражений =D3/D$10, D4/D$10..., при этом в новых дробях изменяется номер строки в числителе, где адрес относительный. Обратите внимание на то, что на построенной ранее круговой диаграмме картофелю соответствует сектор, занимающий 26% площади, а явный расчет дает меньший результат – доля затрат на картофель равна 25,4% общей суммы (см. выше рис. 17).



Для продолжения вычислительной практики рассмотрим новое предположение о том, что заказ на фрукты и овощи был сделан в ценах прошлой недели, а теперь все цены немного изменились, и необходимо переоценить затраты на приобретение прежнего количества продукции.

Чтобы новый расчетный фрагмент таблицы имел на экране компактный и обозримый вид, лучше не заполнять справа новыми формулами большое количество клеток в тех же первых строчках, а разместить еще один экземпляр набора исходных констант в свободных клетках ниже. Например, можно разместить копию блока A1:A9 в таблице, начиная с A13 (выделить A1:A9, команда Правка Копировать, щелкнуть по A13, нажать клавишу ввода), либо ввести в A14 формулу =A2 и методом автозаполнения (мышью за угол) скопировать ее на диапазон A14:C21.

Так будут получены копии значений клеток-источников, а внешний вид их также можно заново не регулировать, а еще раз выделить блок-источник и воспользоваться его форматом как образцом, нажав кнопку Копировать формат панели инструментов Стандартная. Затем нужно только обвести пунктиром диапазон, принимающий копию исходного формата, и освободить кнопку мыши. Теперь можно вписать в таблицу цены новой недели и найти по ним сумму расходов.



Рис.18. Измерение роста цен с помощью индекса фиксированного состава.

Для оценки изменения покупательной способности денег по заданному набору продуктов за истекший период исчисляется сводный показатель – агрегатный индекс цен:



где p – вектор цен продуктов;

q – вектор объемов потребления продуктов (вес покупки).

Задание Рассчитайте по всем продуктам индивидуальные индексы цен , и с учетом долей отдельных продуктов в общей сумме затрат сведите их к агрегатному индексу.

Модуль 2.

Эквивалентность финансовых обязательств





Эквивалентность финансовых обязательств

Приведение размера ожидаемой в будущем денежной суммы к эквивалентной ей величине в более ранний момент времени производится умножением на коэффициент приведения.

Приведенная (текущая, настоящая, современная, дисконтированная) стоимость будущего платежа определяется как размер денежной суммы, которую необходимо инвестировать сегодня для того, чтобы в процессе процентного роста в будущем в указанный момент времени она достигла заданной величины.

Блок 3

посвящен приведению условий договоров к эквивалентному виду, позволяющему проводить сопоставление финансовых результатов на один и тот же момент времени и уровней доходности за одинаковый период.

Блок 4

поможет добросовестному читателю овладеть технологией заполнения электронной таблицы числовой последовательностью с использованием математических законов и моделей роста.

БЛОК 3: Приведение стоимостных показателей к сопоставимому во времени виду

Приведение стоимостных показателей к сопоставимому во времени виду

При изучении этого блока вы узнаете, что такое:

математическое дисконтирование;

эквивалентность условий финансовых контрактов;

средние процентные ставки.

Доверяя Банку 1000 руб. на один год по ставке 30% годовых, вкладчик по истечении срока ожидает получить обратно 1300 руб., при этом обеспечивает себе необходимую в будущем сумму, заблаговременно инвестировав поменьше. При положительном темпе прироста дохода (измеряемом процентной ставкой) за выбранный срок, будущая стоимость денежного вклада всегда больше его начальной величины.

Задание Через 270 дней после подписания кредитного договора должник уплатит 1225,00 руб. Кредит выдан под 30% годовых. Какой была исходная сумма долга, если на него только один раз были начислены простые проценты? 1225,00 = Сложные? 1225,00 = Сложные ежемесячно?

 

Пример. Должник не может выполнить свое обязательство вернуть кредитору в срок 300 000 руб. и предлагает ему удовлетвориться дисконтным векселем Банка номиналом 300 000 руб. со сроком погашения 870 дней, только что приобретенным им по цене 210 000 руб. Кредитор соглашается, и через 9 дней с момента выпуска векселя досрочно предъявляет это долговое обязательство в Банк для погашения. Какую сумму получит кредитор, если при досрочном погашении Банк выплачивает доход по ставке 3% годовых?

Измерим доходность этого векселя годовой ставкой простых процентов R

В случае досрочного погашения Банк вернет цену векселя и уплатит за использование денежных средств в течение 9 дней по ставке 3%, то есть обязательство вернуть 300 000 руб. через 29 месяцев сегодня оценивается значительно дешевле

Сравнение размера денежных сумм, разделенных периодом существенной длины, с точки зрения экономической теории процента, корректно только после их приведения к одному и тому же моменту времени. Правило переоценки текущей стоимости будущего платежа на более ранний момент времени, называется математическим дисконтированием. Понятно, что численное значение текущей стоимости зависит от конкретных возможностей вложения средств на заданный срок – от уровня доходности (величины процентной ставки) и способа начисления процентов. Процентная ставка, с учетом которой оценивается текущая стоимость будущего платежа (путем приведения к меньшей сумме в данный момент времени), называется нормой дисконтирования.

Множитель приведения по сложным процентам PVIF(R,N) = , обратный множителю наращения FVIF(R,N) является вторым основным финансовым коэффициентом, обозначаемым аббревиатурой PVIF (от англ. Present Value Interest Factor – процентный множитель текущей стоимости)





Рис. 19. Построение таблицы множителей приведения PVIF(R,N)

на рабочем листе Excel методом копирования формул.



Рис. 20. Зависимость текущей стоимости 1 000 000 руб.,

ожидаемых через 3 периода, от выбора нормы дисконтирования.

Задание Чему равна текущая стоимость денежной суммы 190 млн руб., ожидаемой через два года при дисконтировании по ставке 6% годовых?

В России в практике принятия инвестиционных решений экономический подход, учитывающий изменение ценности денег во времени, до сих пор соседствует с подходом бухгалтерским, когда общие и средние финансовые показатели за ряд лет исчисляются арифметически без какого-либо дисконтирования. Отчасти это оправдано объективными методическими трудностями при выборе (и особенно прогнозировании!) точного значения нормы сравнения на длительном интервале времени.

Оценка текущей стоимости будущих поступлений и выплат является важным приемом обоснования и принятия решений в инвестиционном анализе. Высокая чувствительность приведенного значения одной и той же будущей суммы к величине процентной ставки, используемой в коэффициенте дисконтирования, заставляет особенно внимательно относиться к выбору методики определения нормы дисконтирования.

Обычно предполагается, что норма дисконтирования должна включать минимально гарантированный уровень доходности доступных инвестору альтернативных вложений капитала, темп инфляции и риск конкретного инвестиционного проекта.

Математически это можно выразить, например, следующей мультипликативной моделью: где R – норма дисконтирования; x – минимально гарантированная доходность; y – уровень инфляции; z – поправка на риск проекта. Приемлемый уровень риска определяется внутренней структурой капитала1 инвестора.

Пример2. Предприятие планирует возвести на своей территории новое здание, и рассматривает предложения, поступившие от двух строительных фирм, конкурирующих между собой за этот заказ. Сметная стоимость здания одинакова – 190 млн. руб. Срок строительства – два года с момента заключения контракта. До завершения строительства требуется вносить авансовые платежи. На непогашенную этими платежами часть стоимости здания после сдачи его заказчику и начала эксплуатации подрядчики предоставляют возможность отсрочки окончательного расчета под льготный процент.



Турецкая фирма "Измир" предлагает внести первый аванс размером 40 млн руб. через год с момента подписания контракта, и второй аванс – 50 млн руб. – через два года, в момент окончания строительства. На оставшуюся сумму 100 млн руб. (исчислена бухгалтером арифметически) предоставляется отсрочка платежа на 1 год по ставке 7% годовых.

Фирма "Иматра" из Финляндии просит внести три авансовых платежа: первый платеж 10 млн руб. сейчас, и еще два одинаковых по 40 млн руб. дважды – через год и в момент сдачи здания заказчику. На оставшуюся часть стоимости здания дается годовая отсрочка под 4% годовых.

Какую сумму достаточно сегодня инвестировать по ставке доходности 10% годовых, чтобы по мере необходимости рассчитываться с подрядчиком в соответствии с условиями контракта? Ответ на этот вопрос дает возможность сравнить предложения на момент принятия решения о выборе подрядчика.





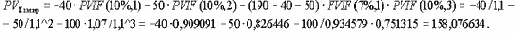
Второе предложение более выгодно фирме-заказчику по критерию минимума суммы затрат, приведенных к начальному моменту времени.



Рис. 21. Распределение затрат на строительство во времени.

Приведение вариантов к сопоставимому виду необязательно ориентировать на более ранний момент времени, можно их сравнивать, например, по критерию будущей стоимости, которую можно нарастить на банковском счете под заданный процент, за счет отказа от расходов по контракту. В общем случае платежи можно сравнивать применительно к любому моменту времени внутри срока данного финансового обязательства. Давайте оценим текущую стоимость контракта "Иматра" на момент окончания строительства (год 2) по ставке сравнения 10% годовых.



Проверка



Текущая стоимость эквивалентна

, относящейся к моменту времени "два периода назад" при сравнении по норме доходности 10% сложных за один процентный период.

Задание Предположим, что фирма "Измир" до подписания контракта узнала о том, что предложение ее конкурента с точки зрения заказчика более приемлемо, и решила снизить процент за отсрочку последнего платежа с 7% до 5%. Найдите текущую стоимость платежей предприятия этому подрядчику при новых условиях контракта. Сравните также контракты "Иматра" и "Измир 5%" на момент полного погашения долга (год 3) при дисконтировании по ставке 9% годовых. Необходимые для расчетов значения множителей приведения PVIF(9%,N), обратные множителям будущей стоимости FVIF(9%,N), можно найти в рабочей таблице на рис. 19.

<


Финансовые операции считаются эквивалентными, если суммы дохода по ним, приведенные к одному и тому же моменту времени, совпадают.

Финансовые операции считаются эквивалентными по уровню доходности, если их эффективные ставки (или будущие стоимости единичной инвестиции по прошествии года) совпадают.

Процентные ставки называются эквивалентными, если при замене в контракте одной из них на другую за тот же срок финансовые результаты не изменятся.

Эквивалентные друг другу значения сравниваемых между собой процентных ставок обычно выводятся из уравнения эквивалентности – условия равенства множителей наращения за одно и то же время начисления процентов.

Пример. Найдем, годовую ставку обыкновенных сложных процентов с ежедневным начислением, эквивалентную годовой доходности 30,8%. Искомую номинальную величину ставки R можно выразить явно из соотношения



В случае возникновения технических проблем с извлечением корня 360 степени можно решить это уравнение итеративно - подбором искомого значения R методом проб и ошибок.

Для нахождения процентных ставок, эквивалентных на заданном интервале времени переменным ставкам, применяются средние процентные ставки, метод вычисления которых зависит от выбранного правила начисления процентов. Формула среднего выводится из уравнения эквивалентности.

Задание Какой силе роста при непрерывном начислении процентов эквивалентна годовая доходность 30,8%? Какая годовая ставка простых процентов эквивалентна ставке 60% сложных годовых при их ежеквартальном начислении в течение полутора лет? В течение одного года (см. рис. 22)?

 

Средняя ставка простых процентов определяется из условия равенства множителей наращения за полный срок N, равный сумме более мелких интервалов времени , на которых переменная процентная ставка сохранялась постоянной на уровнях соответственно.





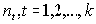
Рис. 22. Равенство множителей наращения по эквивалентным ставкам за 1 год = 4 квартала.

Пример. По вкладам до востребования в рублях с начала 1999 г. действовала ставка 3%, с 1 декабря 1999 г. она была снижена до 2%, а с 21 марта 2000 г. до 1% годовых.



Найдем среднюю ставку простых процентов за период с 01/05/1999 по 01/05/2000 (два варианта организации вычислений в таблице см. на рис. 23).



Рис. 23. Средняя процентная ставка, взвешенная по периодам действия.

Средняя ставка простых процентов есть арифметическая средняя с весами, равными длительности отдельных периодов.

Задание Используя данные табл. 9, найдите среднее значение учетной ставки ЦБ РФ с 01/04/99 по 01/04/00.

Таблица 9

Новейшая динамика процентной ставки рефинансирования ЦБ РФ по кредитам3

Период действия	% годовых
24/07/98 – 09/06/99	60%
10/06/99 – 23/01/00	55%
24/01/00 – 06/03/00	45%
07/03/00 – 20 03/00	38%
21/03/00 – 09/07/00	33%
10/07/00 – 03/11/00	28%
04/11/00	25%

Средняя ставка сложных процентов является корнем уравнения, поэтому множитель будущей стоимости по средней ставке сложных процентов находится по формуле взвешенной средней геометрической.

.

Пример. Среднемесячный темп инфляции за 10 месяцев 2000 г.

Используя приведенные на рис. 24 данные Госкомстата РФ4 об изменении индекса потребительских цен, оценим показатель инфляции за месяц, то есть найдем такой среднемесячный темп роста индекса потребительских цен h, что



где t – порядковый номер месяца в 2000 г., t = 1, … ,10;

bt – базисный индекс цен в месяце t по сравнению с декабрем 1999 г. (t

= 0);

ct – цепной индекс цен в месяце t по сравнению с предыдущим месяцем t – 1.



Рис. 24. Динамика показателя инфляции за 10 месяцев 2000 г.

Здесь показан вариант организации рекуррентного табличного вычисления базисного за период t индекса bt

как произведения цепного индекса данного периода се на базисный индекс предпоследнего периода bt-1 с учетом того, что b1 = c1. В результате получено значение b10 = 116,5%. Cреднемесячный индекс потребительских цен (1 + h) находим по формуле среднего геометрического, приняв длину каждого месяца за постоянную величину (1 месяц = 30 дней). При этом предположении в формуле средневзвешенного среднего геометрического все весовые показатели nt = 1, а их сумма N = 10. Тогда





Для переоценки с учетом инфляции стоимости основных фондов и имущества в момент реализации используется дефлятор ИРИП (Индекс стоимости Реализуемого Имущества Предприятия)5. На рис. 25. показано поквартальное увеличение реальной стоимости имущества, приобретенного в начале 1998 г. по цене 80 млн. руб., к моменту реализации в начале 2001 г. (без учета амортизации).



Рис. 25. Рост реальной стоимости имущества с учетом инфляции.







1 См.: Бригхем Ю., Гапенски Л. Финансовый менеджмент / Пер.с англ. СПб., 1998.

2 Пример является переработанной задачей из кн.: Бухвалов А.В., Идельсон А.В. Самоучитель по финансовым расчетам. М., 1997.

3 Источник: «АКДИ Экономика и жизнь» – www.akdi.ru/finance/refin/akdi.htm

4 Источник: «АКДИ Экономика и жизнь» – www.economics.ru/econom/

5 Источник: «АКДИ Экономика и жизнь» – http://www.akdi.ru/econom/stat/def_1.htm

БЛОК 4: Моделирование роста числовой последовательности в таблице

Моделирование в таблице роста числовой последовательности

Проработав задания этого блока на персональном компьютере, вы:

освоите несколько способов заполнения блока таблицы числовой последовательностью с заданным законом роста;

закрепите навыки построения и копирования расчетных формул;

научитесь использовать формулы массива и таблицы подстановки.

Рост ценности денег во времени при начислении сложных процентов подчиняется геометрическому закону, а правило простых процентов производит арифметическую прогрессию. Пользователю электронных таблиц Excel предоставляется избыточное число способов организации вычислений значений элементов этих числовых последовательностей.

Простейшим способом получения арифметической прогрессии в блоке клеток таблицы является операция автозаполнения с помощью мыши, источником данных, для которого служит выделение в таблице двух смежных клеток, содержащих значения двух последовательных членов прогрессии.

Разность арифметической прогрессии при этом вычисляется автоматически и используется программой как постоянный шаг для заполнения блока числовыми константами. Знак шага прогрессии определяется по направлению движения мыши: от меньшего числа в сторону большего – шаг положительный, то есть рост, а от большего к меньшему – снижение. Этот способ обычно применяется для быстрого получения последовательности порядковых номеров.

Задание Постройте таблицу порядковых номеров дней високосного года по образцу табл. 2. методом копирования формул методом автозаполнения. Сколько дней между датами 23/02 и 08/03?

Геометрическую прогрессию при помощи автозаполнения получить в Excel нельзя, но она является одним из типов числовой последовательности, которыми можно заполнить блок клеток и без ввода в таблицу явных формул, если использовать команду Правка Заполнить Прогрессия...

Рис. 26. Диалоговое окно команды Правка Заполнить Прогрессия...

Задание Постройте таблицу порядковых номеров дней марта месяца невисокосного года, заполнив вертикальный блок клеток значениями арифметической прогрессии. Чему равен первый член этой прогрессии?

<
Правила начисления процентов также могут быть выражены рекуррентно. Рассмотрим динамику роста денежного вклада при простых, и при сложных процентах. Выбор варианта рекуррентной формулы, с помощью которой можно представить правило начисления процентов, дающее в результате одну и ту же числовую последовательность (см. рис. 28), зависит от навыков пользователя Excel, глубины его абстрактного мышления, и потребностей решаемой задачи. Обзор простейших альтернатив организации вычислений приводится в табл. 10.

Таблица 10

Варианты рекуррентного кодирования правил начисления процентов

	Рост по правилу
Процентная ставка выражена	простых процентов	сложных процентов
числовой константой 0,15	=C3+0,15*C$3	=D3+0,15*D3 или =1,15*D3
абсолютной ссылкой B$1	=C3+B$1*C$3	=D3+B$1*D3
именем ячейки ставка	=C3+ставка*C$3	=(1+ставка)*D3

Рис. 27. Модели роста стоимости вклада.

Пример расположения данных на рабочем листе и кодирования необходимых вычислений приведен на рис. 27 в режиме вывода формул. Найденные по этим формулам числовые значения даны на рис. 28.

При использовании рекуррентных формул в процентных вычислениях номера периодов в явном виде в расчете не участвуют, а выполняют в таблице только роль поясняющих надписей. Номер процентного периода (и соответствующего члена прогресии) станет влияющим параметром при другом подходе – расчете на основе общей формулы члена прогресии.



Рис. 28. Числовые значения формул, предложенных на рис. 27.

Пример. Текущая стоимость потока будущих затрат.

Текущая стоимость представляет собой дисконтированную сумму будущих затрат. Дисконтирование производится делением на процентный множитель величина которого зависит от числа процентных периодов, разделяющих моменты осуществления затрат и текущей оценки. Каждый следующий процентный множитель легко рекуррентно получать из предыдущего умножением на знаменатель геометрической прогрессии (1+R), где ставка за один период R=10%.



Рис. 29. Рекуррентная модель вычисления текущей стоимости потока будущих платежей.

Задание Используя данные рис. 30 и рис. 24 как образец расчета средней ставки простых процентов, взвешенной по периодам действия, найдите среднее значение ставки рефинансирования ЦБ РФ за указанный период.

<




Рис. 30. Динамика ставки рефинансирования ЦБ РФ в 1996–1998 гг.

Пример. Зависимость срока удвоения вклада при начислении сложных процентов от ставки.



Известен следующий упрощенный способ вычисления срока удвоения вклада при начислении сложных процентов по постоянной ставке R: число 72 делится на число сотых долей в процентной ставке и получается срок удвоения ("правило 72").



Рис.31. Сравнение точной формулы срока удвоения вклада по сложным процентам и "правила 72".

Действительно (см. рис. 31), при малых R эта функция хорошо аппроксимирует искомую логарифмическую, тем более, что получаемое значение срока обычно нужно округлять вверх до целого числа.

Пример. Последовательность чисел Фибоначчи6 задается двумя своими первыми членами, равными единице, и правилом: каждое новое число равно сумме двух предыдущих.

Для получения в строке электронной таблицы начала последовательности чисел Фибоначчи достаточно задать в отдельных клетках два первых единичных значения, закодировать их адресами формулу, и скопировать ее направо – см. рис. 32.



Рис. 32. Табличная формула, моделирующая последовательность чисел Фибоначчи.

Пример . Число возможных перестановок из N элементов равно произведению всех натуральных чисел от 1 до N. Это произведение называется N-факториал и обозначается N! = 1*2*...*N.

По определению, 1!=1. Затем верно рекуррентное правило (N + 1)! = (N + 1) * N!



Рис. 33. Рекуррентная табличная модель расчета N!

Пример. Инвестор вносит сумму 5 млн руб на счет с начислением сложных процентов по ставке 8% за период., и затем дважды в конце каждого расчетного периода добавляет на счет столько же.

Какую сумму удастся таким образом нарастить за 3 периода?

Таблица 11

Будущая стоимость потока платежей (млн руб.)

Период	Сумма вклада с процентами в конце периода	Новый платеж в конце периода	Переходящий остаток на счете в конце периода
1	0,000 =	5,000	5,000 = 0,000 + 5,000
2	5,400 =	5,000	10,400 = 5,400 + 5,000
3	11,232 =	5,000	16,232 = 11,232 + 5,000

<


При какой процентной ставке те же три платежа по 5 млн руб. каждый, регулярно вносимые на счет в конце периода, позволят накопить сумму не 16,232 млн руб., а 20,000 млн руб.? Чтобы ответить на этот вопрос нужно составить уравнение и выразить из него искомую ставку R.



Рис. 34. График левой части квадратного уравнения.

В данном примере уравнение является квадратным (см. рис. 34) и имеет два решения. Значение искомой ставки процентов доставляет положительный правый корень.

Если многочлен в левой части такого уравнения имеет высокий порядок N (число элементов потока платежей), то решений может быть несколько, а единой формулы для нахождения корней не существует. Поэтому ставку подбирают итеративно. Подбор нулевого значения левой части дает ответ R = 56,16%.

Пользователю Excel для нахождения этого ответа достаточно вызвать процедуру Сервис, Подбор Параметра (см. рис. 35). Как хорошо видно на рис. 34, правый корень находится между значениями 0,50 и 0,75. В свободную клетку таблицы, например B24, помещаем начальное приближение 0,60.

В соседнюю клетку C24 вводим формулу левой части уравнения, где место неизвестной ставки R занимает ссылка на влияющую клетку B24. Процедура Подбор Параметра (Goal Seek) итеративным подбором установит (Set cell) в зависимой ячейке (клетка C24 с расчетной формулой левой части уравнения) искомое значение (To value) 0, изменяя значение (By changing cell) влияющей ячейки (клетка B24).



Рис.35. Диалоговое окно процедуры Подбор параметра в оригинальной версии Excel.

Если организовать вычисления не по рекуррентной, а по общей формуле члена прогрессии, то именно номер члена становится ведущим расчетным параметром, поскольку формульное выражение явно ссылается на номер текущего периода. Значения формул меняются в зависимости от номеров моментов времени, ограничивающих периоды.

В левой части окна на рис.36 использована формула массива (со ссылкой на интервал A2:A9 значений параметра N – срок), а справа – обычная техника копирования формул.





Рис. 36. Модели организации табличных вычислений по общей формуле члена прогрессии.

Дальнейшим развитием идеи организации на рабочем листе блоков данных, табулирующих влияние частного изменения параметра на значение исследуемой функции, является процедура создания таблиц "анализа чувствительности" (англ. What-If Analysis), инициируемая командой Данные, Таблица подстановки...

Правила использования этой процедуры Excel требуют такой записи расчетных формул, чтобы они не содержали ссылок ни на какие внутренние ячейки области создаваемой таблицы, в том числе не ссылались и на клетки с числовыми значениями параметра. Чтобы математические выражения при этом все-таки можно было как-то закодировать, договорились внутри формулы на месте параметра ставить "местоимение" – адрес ячейки ввода.



Рис. 37. Определение таблицы подстановки, данное в Справочной системе Microsoft Excel.

Ячейкой ввода может быть, независимо от содержимого, любая ячейка рабочего листа вне области таблицы подстановки. Попробуем представить два правила начисления процентов как таблицу подстановки "с одной ячейкой ввода", то есть с одним параметром, каковым является в данном случае дискретно заданное время.

До вызова этой процедуры необходимо, чтобы уже был заполнен значениями параметра интервал смежных клеток столбца (в блок B3:B10 записаны номерами периодов от 0 до 7), и на одну строку выше первого значения параметра в столбцах правее располагаются формулы табулируемых функций, ссылающиеся на ячейку ввода..

а) режим вывода значений

б) режим вывода формул

Рис. 38. Внешний вид таблицы подстановки значений одного параметра в две формулы.

Моменты времени занумерованы на рабочем листе вертикально, то есть влияющий параметр меняется по строкам внутри одного столбца. Поэтому адрес выбранной ячейки ввода нужно сообщить во втором поле ввода диалогового окна, оставив первое поле пустым.

Если интервал значений параметра таблицы подстановки на рабочем листе располагается горизонтально, то отвечать необходимо наоборот, только на первый вариант вопроса. Ссылаться на обе ячейки ввода пользователю приходится при построении таблиц подстановки, зависящих от двух параметров.



Пусть, например, ячейкой ввода будет F8. В клетку C2 введем знакомую формулу простых процентов =1+0,15* F8, а в клетку D2 – сложных =1,15^ F8. Далее нужно выделить всю область таблицы подстановки – блок B2:D10 и применить команду Данные Таблица подстановки...

При необходимости изменить расчетную формулу, например поставить 20% вместо 15%, теперь достаточно отредактировать выражение только в формуле верхней строки таблицы подстановки.

Задание Заполните блок клеток рабочего листа электронной таблицы колонками значений и постройте по ним диаграммы роста стоимости одной денежной единицы, вложенной на срок 18 месяцев по ставке 24% годовых при начислении процентов: сложных ежемесячно; простых ежемесячно; простых ежемесячно с реинвестированием каждые полгода; сложных ежеквартально; сложных за полный год и простых за дробную часть года. Постройте искомые таблицы значений будущая стоимость разными методами: по рекуррентной формуле; по общей формуле копированием; по общей формуле массива; по общей формуле как таблицу подстановки; заполнением блока прогрессией чисел.

Пользователь Excel имеет возможность организовать на рабочем листе таблицу значений функции не только одного, но и двух аргументов (параметров), причем также несколькими способами. В качестве примера для построения таблиц подстановки с двумя параметрами возьмем таблицы финансовых коэффициентов.

Ранее было рассмотрено построение таблицы дисконтирующих множителей PVIF(R,N) для 4% < R < 10% с шагом 1% для N=1, 2, 3 методом копирования формул. Например, в клетку B3 помещается выражение =1/(1+B$2)^$A3, которое кодирует правило построения таблицы: "считаем число, обратное сумме единицы и ставки процента, возведенной в степень, заданной как срок; причем значение процента берем всегда из самой верхней строки, а срок – всегда из крайней левой колонки".

Для поддержания единства блока клеток, заполненного одной формулой, методу копирования формул лучше предпочесть встроенную процедуру Данные Таблица подстановки... и построить с её помощью таблицу-массив с двумя параметрами.



Начинать изготовление таблицы значений множителей наращения, показанной на рис.39, нужно с заполнения части столбца A3:A5 рядом значений срока и части строки B2:H2 последовательностью значений ставки сложных процентов. После этого в левый верхний угол области будущей таблицы подстановки (ячейка A2) вводится расчетная формула, в которой в роли ссылок на параметры выступают адреса двух ячеек ввода, внешних по отношению к области таблицы. В качестве ячейки, куда будет подставляться процентная ставка, выбрана A1, а ссылка на срок заменяется обращением к ячейке E1. Расчетная формула в клетке A2 имеет вид =(1+A1)^E1. Затем необходимо выделить блок ячеек A2:H5 и дать команду Данные Таблица подстановки...



Рис. 39. Множители наращения сложных процентов FVIF(R,N).



Рис. 40. Построение таблицы данных с двумя параметрами.

В первое поле ввода диалогового окна рис.41, щелчком мыши помещена абсолютная ссылка на ячейку A1, занимающую в производящей формуле таблица параметр R – процентную ставку, значения

которой расположены над таблицей горизонтально, то есть меняются по столбцам внутри одной строки.

Во втором поле ввода нужно дать ссылку на ячейку E1, куда будут подставляться значения параметра N – срок, интервал изменения которого задан слева вертикально, то есть в одном столбце по строкам.

6 Итальянский монах и математик Леонардо из Пизы, более известный под именем Фибоначчи (сын Боначчи). Фибоначчи познакомил Европу с достижениями индийской (арабской) математики. Именно он ввел в обиход арабские цифры и позиционную десятичную систему счисления, чем положил начало эпохи коммерческой арифметики в средние века. См.: Соколов Я.В. Бухгалтерский учет: от истоков до наших дней. М., 1996.

Модуль 3.

Оценка параметров потоков платежей





Оценка параметров потоков платежей

В финансовой практике широко распространены контракты, предусматривающие не разовое, а систематическое движение средств – выплаты/поступления по заданному графику происходят регулярно.

Последовательность платежей, разделенных равными интервалами времени, называется равномерной

финансовой рентой или потоком платежей. Поток платежей одинакового размера называется постоянной финансовой рентой или аннуитетом (англ. annuity). Если платежи неодинаковы по знаку и размеру, то применяется более общий термин денежный поток (от англ. cash flow).

Блок 5 посвящен методике математического дисконтирования денежного потока будущих доходов/расходов инвестиционного проекта и построенным на её основе критериям эффективности капиталовложений.

Блок 6 знакомит читателя с широко применяемым в финансовом анализе понятием аннуитета и возможностями автоматизации стандартных вычислений с использованием встроенных функций Excel.

БЛОК 5: Денежный поток инвестиционного проекта

Денежный поток инвестиционного проекта

При изучении материала этого блока вы узнаете, что такое:

дисконтированный доход;

чистый дисконтированный доход;

индекс рентабельности инвестиций;

внутренняя норма доходности.

Методы измерения доходности инвестиционных проектов основаны на анализе равномерного денежного потока. Ожидаемые значения элементов денежного потока, соответствующие будущим периодам, являются результатом сальдирования всех статей доходов и расходов, связанных с осуществлением проекта.

Для приведения значений элементов денежного потока к сопоставимому во времени виду по выбранной норме дисконтирования оценивается суммарная текущая стоимость на момент принятия решения о вложении капитала, предшествующий началу движения средств. Уровень процентной ставки, применяемой в качестве нормы дисконтирования, должен соответствовать длине периода, разделяющего элементы денежного потока.

Чистый дисконтированный доход показывает, превышает ли текущая стоимость ожидаемых доходов/расходов по проекту (дисконтированный доход) инвестиционные затраты в начальный момент времени. В англо-американских учебниках по финансовому менеджменту этот показатель называется Net Present Value, поэтому формула его расчета, встроенная производителями вычислительной техники в компьютерные программы и даже в финансовые калькуляторы, стандартно идентифицируется аббревиатурой NPV.

Пример. Найти чистый дисконтированный доход1 проекта, требующего стартовых инвестиций в объеме 100 тыс руб., денежный поток которого задан рис. 41, по ставке сравнения 10% годовых.

Рис. 41. Денежный поток проекта.

Рис. 42. Чистый дисконтированный доход.

Обозначим элементы денежного потока Z1,Z2,…,ZN

в соответствии с моментами времени, а инвестиционные затраты нулевого периода – Z0.

На рис. 43 этот расчет представлен двумя способами. Промежуточные вычисления в колонках E и F соответствуют рекуррентной модели (элементы денежного потока перемножаются на множители приведения).

Готовый результат 109,050 в одной клетке дает табличная формула =NPV(10%;C4:C11), вызывающая специальную финансовую функцию со ссылкой на норму дисконтирования и табличные координаты блока значений элементов денежного потока, расположенных в хронологическом порядке.

Рис. 43. Диалоговое окно финансовой функции NPV в оригинальной версии Excel.

Необходимо заметить здесь, что, несмотря на название, функция NPV вычисляет не весь чистый, а только дисконтированный доход, то есть Present Value денежного потока (на один период назад от первого поступления/выплаты). Эту особенность табличной функции NPV

удобно использовать в расчете индекса рентабельности (англ. profitability index) инвестиционного проекта, относя дисконтированный доход по нему к начальным затратам Z0<0.

.

В рассматриваемом примере индекс рентабельности проекта 109%=109,05/100. Это значение можно вычислить по формуле =-NPV(E1;C4:C11)/C3.

Для вычисления чистого дисконтированного дохода к выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных затрат нулевого периода, записанное в таблице в ячейке C3 (см. формульное выражение в строке ввода над полем рабочего листа на рис.42).

В русифицированной версии Excel (ниже 2000) финансовые функции получили такие идентификаторы, которым далеко не всегда удается поставить в соответствие финансовые термины. Так, например, функция для вычисления дисконтированного дохода в локализованной версии Excel переименована в НПЗ (см. рис. 44).



Рис. 44. Диалоговое окно функции NPV=НПЗ.

Несмотря на то что аббревиатура НПЗ в русском языке не расшифровывается ни в какое приемлемое в качестве финансового термина словосочетание, для работы в локализованной версии пользователю придется запомнить именно этот стандартный идентификатор. Читатель, владеющий английским языком, может также самостоятельно убедиться в неадекватности представленного в диалоговом окне перевода смыслу вложенной в эту функцию модели. По-русски более правильно было бы написать, что функция "Возвращает чистый

дисконтированный доход инвестиционного проекта, вычисляемый по выбранной норме дисконтирования и потоку будущих выплат (отрицательные значения в денежном потоке) и поступлений (положительные значения). Норма:

процентная ставка, принятая в качестве нормы дисконтирования и соответствующая продолжительности единичного периода времени, разделяющего соседние элементы денежного потока инвестиционного проекта". Пояснения справочной системы Excel на русском языке (см. рис. 45) также "не дружат" с финансовой терминологией. В Excel 97 можно добавить к этой справке собственные пояснения, использовав команду Параметры Заметки…





Рис. 45. Дополнение встроенной справочной информации Excel 97

заметками пользователя, уточняющими контекст.

Таблица 13

Сравнение двух проектов, требующих одинаковых вложений капитала

	Проект 1	Проект 2
Инвестиции 0 года	-1000	-1000
Доход 1 года	200	200
Доход 2 года	300	400
Доход 3 года	600	700
Доход 4 года	500	400
Доход 5 года	100	0
Дисконтированный доход по ставке 19%
Дисконтированный доход по ставке 21%	980,69	1020,23
Дисконтированный доход по ставке 24%
Чистый дисконтированный доход по ставке 19%
Чистый дисконтированный доход по ставке 21%	-19,31	+20,23
Чистый дисконтированный доход по ставке 24%
Индекс рентабельности при ставке 19%
Индекс рентабельности при ставке 21%	98%	102%
Индекс рентабельности при ставке 24%

Задание Сравните два проекта, денежные потоки которых представлены в табл. 13, при значениях ставки сравнения 19% и 24%. Впишите ответы в свободные клетки табл. 13. Подберите такое значение нормы дисконтирования, при которой чистый дисконтированный доход второго проекта равен нулю.

Задание Как оценить срок окупаемости инвестиционного проекта (см. рис. 46)? Какой срок окупаемости короче – простой или дисконтированный?

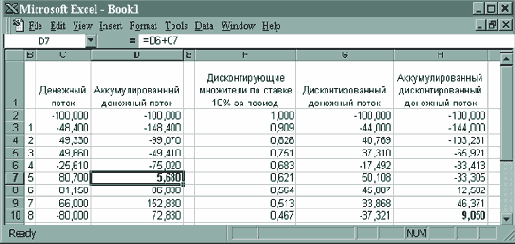
Рис. 46. Определение простого и дисконтированного сроков окупаемости проекта.

Важным критерием принятия инвестиционный решений на основе дисконтирования денежного потока является внутренняя норма доходности (англ internal rate of return). Это такое значение нормы математического дисконтирования, при котором текущая стоимость денежного потока абсолютно равна инвестициям. Внутренняя норма доходности является корнем IRR

неявного уравнения, в левой части которого стоит многочлен (полином) степени N.



Из основной теоремы алгебры следует правило знаков Декарта, в соответствии с которым число положительных вещественных корней многочлена, включая кратные, равно k



– числу перемен знака в ряду коэффициентов многочлена, или k минус положительно чётное число. Если k = 1, то уравнение имеет единственное положительно решение.

Следствием правила знаков Декарта является следующее утверждение: если Z0<0 и все Z1,…,ZN³ 0, то существует единственное решение (1+IRR) > 0, то есть IRR > –1.

IRR > 0 при условии

Справедливо также правило Норстрёма2, сформулированное через число перемен знака в ряду элементов аккумулированного денежного потока (см. рис. 46): если последний член аккумулированного денежного потока не равен нулю, и при этом в ряду значений элементов аккумулированного денежного потока знак меняется только один раз, то для исходного денежного потока существует единственное положительное значение внутренней нормы доходности IRR.

Денежный поток, имеющий единственное положительное значение внутренней нормы доходности IRR, называется регулярным.

Найти значение внутренней нормы доходности в Excel можно подбором параметра (см. рис. 45), или встроенной финансовой функцией IRR = ВНДОХ (см. рис. 46).



Рис. 45. Подбор значения внутренней нормы доходности.



Рис. 48. Вычисление внутренней нормы доходности встроенной функцией IRR = ВНДОХ.

Первый аргумент этой функции – табличный интервал ячеек, где в хронологическом порядке расположены элементы денежного потока, начиная с нулевого. Именно к этому значению программа будет подгонять дисконтированный доход, изменяя процентную ставку. Второй необязательный аргумент (значение 10% установлено по умолчанию) задает предполагаемый ответ для начала итеративной процедуры приближенных вычислений.

1 Коссов В.В., Лившиц В.Н., Шахназаров А.Г. Методические рекомендации по оценке эффективности инвестиционных проектов: официальное издание. М., 1999.

2 Сюдсэтер К., Стрём А., Берк П. Справочник по математике для экономистов. СПб., 2000.

БЛОК 6: Аннуитетные финансовые функции

Аннуитетные финансовые функции

При изучении материала этого блока вы узнаете, что такое:

потоки платежей постнумерандо и пренумерандо;

вечная рента (бессрочный аннуитет) и срочный аннуитет;

текущая и будущая стоимость аннуитета;

процентная ставка за период между платежами;

погашение долга равными платежами;

равномерное погашение долга.

Аннуитетом называется поток платежей одинакового размера, поступающих через равные промежутки времени. Период времени между двумя последовательными платежами является расчетным при начислении процентов.

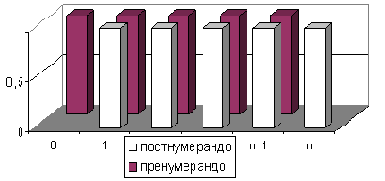
Рис. 49. Тип аннуитета задает распределение n платежей одинакового размера

по границам процентных периодов внутри срока аннуитета.

В зависимости от момента поступления первого платежа различают два типа потоков платежей – пренумерандо (первый платеж в начале первого периода) и постнумерандо (в конце). За счет более раннего поступления денежных средств и удлиненного на один период срока начисления процентов в случае пренумерандо можно достигнуть больших финансовых результатов по сравнению с потоком платежей, вносимых в конце периода.

Пример. Пять платежей по три рубля каждый нужно внести по схеме пренумерандо. Получатель аннуитета использует эти средства с доходностью R = 8% за период между платежами.

Какова будущая стоимость FV этого срочного аннуитета (срок n = 5) в конце пятого периода в результате начисления процентов на все поступившие платежи? Обозначим размер одного платежа буквой A. Тогда

В условиях нашего примера поток платежей пренумерандо позволяет их получателю накопить сумму 19,01 руб., а в случае аннуитета постумерандо она бы составила только 17,60 руб. (см. рис. 50) .

Рис. 50. Вычисление будущей стоимости каждого платежа и аннуитета пренумерандо в конце срока.

Задание Какую сумму достаточно вложить на 5 периодов с начислением 8% сложных, чтобы в конце срока снять 19,01 руб.?

Текущая стоимость бессрочного аннуитета (вечной ренты при бесконечно большом сроке n) есть сумма всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0 сходится.

Формула текущей стоимости срочного аннуитета постнумерандо для n < ¥ выводится как разница текущей стоимостей двух бессрочных аннуитетов. Из текущей стоимости на момент времени 0 вечной ренты постнумерандо вычитается текущая стоимость такой же вечной ренты, начинающейся на n периодов позже. Вторая стоимость численно равна первой, но относится к моменту времени n, поэтому перед вычитанием её необходимо дисконтировать по той же ставке R

на n периодов в прошлое.



Эквивалентная ей в конце срока будущая стоимость срочного аннуитета постумерандо есть

Процентный множитель будущей стоимости аннуитета FVIFA(R,n) – Future Value Interest Factor of Annuity является основным финансовым коэффициентом, который показывает, какую сумму можно накопить, постоянно получая выплаты единичного размера в течение срока n при начислении R % сложных за каждый период на уже аккумулированные денежные средства.

Процентный множитель текущей стоимости аннуитета PVIFA(R,n) – Present Value Interest Factor of Annuity также является финансовым коэффициентом, и показывает, какую сумму достаточно инвестировать в начальный момент времени, чтобы потом регулярно в течении срока, состоящего из n процентных периодов получать платежи единичного размера с учетом начисления на оставшиеся денежные средства R% сложных за период.

Знакомство с условностями автоматизации финансовых расчетов в среде процессора электронных таблиц начнем со встроенной функции =FV(rate; nper; pmt; pv; type)

=БЗ(норма; число_периодов; выплата; нз; тип).

Пример. Господин Иванов в конце каждого месяца переводит 1000р. за счет в банк, начисляющий ежемесячно сложные проценты по номинальной ставке 9% годовых. Какая сумма накопится на счете за два года, при сохранении на это время всех указанных условий без изменения?



Рис. 51. Применение функции БЗ=FV для расчета будущей стоимости аннуитета.

Выполним арифметические вычисления поэтапно. Ниже, на рис. 52, в восьмой строке таблицы рабочего листа дан формат вызова функции =БЗ, возвращающий то же самое числовое значение, которое в ячейке седьмой строки найдено по рекуррентным формулам.





Рис. 52. "Аннуитетный треугольник" постнумерандо.

В зависимости от выбора пользователем из полного списка аргументов встроенной функции =БЗ(норма; число_периодов; выплата; нз; тип) подмножества тех аргументов, значения которых известны в задаче, можно с помощью одной и той же функции посчитать и наращенную сумму вклада, и будущую стоимость аннуитета, причем с переключением формул между типами потоков платежей постнумерандо и пренумерандо.

Рассмотрим полностью возможные варианты.

1,46 р. = FV(0,1;4;0;-1;0) =БЗ(0,1;4;0;-1;0) =БЗ(0,1;4;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после четырех раз (число_периодов=4) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% (норма=0,1) без дополнительных поступлений и выплат. В связи с полным отсутствием в течение срока промежуточного потока платежей нет смысла уточнять и момент их поступления в нулевом размере (тип=0, значение используется по умолчанию).

1,61 р. =FV(0,1;5;0;-1;0) =БЗ(0,1;5;0;-1;0) =БЗ(0,1;5;;-1) – будущая стоимость одного вложенного рубля (нз=-1) после пяти раз (число_периодов=5) присоединения к нему процентных денег, начисляемых в конце периода по ставке сложных процентов 10% (норма=0,1) без дополнительных поступлений и выплат (выплата=0, тип=0).

6,11 р. = FV(0,1;5;-1;0;0) БЗ(0,1;5;-1;0;0) =БЗ(0,1;5;-1) – будущая стоимость потока пяти периодических платежей (число_периодов=5) единичного размера, вносимых (выплата=-1) регулярно в конце периода (потоку постнумерандо

соответствует тип=0, значение используется по умолчанию) при начислении 10% сложных (норма=0,1) за период между моментами внесения платежей на поступившие ранее средства.

6,72 р. = БЗ(0,1;5;-1;0;1) БЗ(0,1;5;-1;0;1) =БЗ(0,1;5;-1;;1) – будущая стоимость потока пяти периодических платежей (число_периодов=5) единичного размера (выплата=-1), поступающих в начале периода (потоку пренумерандо

соответствует тип=1) при начислении за каждый период между платежами 10% сложных (норма=0,1).



Таблица 14

Аннуитетные финансовые функции

Показатель	Встроенная функция Excel
Будущая ценность	БЗ(норма;число_периодов;выплата;нз;тип)
Future value	FV(rate;nper;pmt;pv;type)
Сегодняшняя ценность	ПЗ(норма;кпер;выплата;бс;тип)
Present value	PV(rate;nper;pmt;fv;type)
Периодический платеж	ППЛАТ(норма;кпер;нз;бс;тип)
Payment	PMT(rate;nper;pv;fv;type)
Количество периодов	КПЕР(норма;выплата;нз;бс;тип)
Number of periods	NPER(rate;pmt;pv;fv;type)
Процентная ставка	НОРМА(кпер;выплата;нз;бс;тип;предположение)
Interest rate	RATE(nper;pmt;pv;fv;type;guess)

Пример. Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15 долл. на сберегательный счет в банк, начисляющий на всю растущую сумму сложные проценты по номинальной ставке 15% годовых. В каком возрасте этот человек может стать миллионером?

Выразим срок (число периодических платежей) из формулы будущей стоимости аннуитета:

Задание Используя определение и свойства логарифма, самостоятельно продолжите вывод формулы срока накопления миллиона в условиях задачи и найдите ответ на поставленный вопрос.

Рис. 53. Применение функции КПЕР=NPER для определения срока аннуитета.

Найденный срок выражен в месяцах. 542/12=45 полных лет, так что сумма 15+45 дает искомый в задаче возраст 60 лет.

Какую сумму достаточно вложить на такой же срок единовременно, чтобы при той же доходности при ежемесячном начислении сложных процентов накопить 1 млн.долл.?

Ответ: -1190,948=PV(0,15/12;542;;1000000).

При какой годовой процентной ставке удастся накопить миллион к 55 годам?

Ответ: 17,3% =RATE((55-15)*12;-15;;1000000)*12.

При каком размере ежемесячного платежа удастся накопить миллион к 50 годам без изменения ставки 15%?

Ответ: -68,13 долл.= PMT(0,15/12;(50-15)*12;;1000000).



Варьировать параметры задачи можно и неявно, подгоняя влияющие исходные данные, например, размер ежемесячного платежа, под искомую будущую стоимость 1 млн.долл. (см. рис. 54).





Рис. 54. Подбор значения будущей стоимости аннуитета изменением размера платежа.

Неявное уравнение, используемое всеми финансовыми калькуляторами и электронными таблицами для расчета неизвестных показателей аннуитета по известным можно обнаружить в Справочной системе Excel в разделе, посвященном функции =ПЗ. Для преодоления проблем с терминологией здесь оно приводится в обозначениях оригинала:



Таблица 15

Реакция неявного уравнения на нулевые значения финансовых параметров

Наращение однократно вложенной суммы	Накопление будущей суммы потоком вносимых через равные периоды времени платежей одинакового размера
Если в условиях задачи отсутствует поток выплат, то PMT=0, и за счет нулевого первого сомножителя всё второе слагаемое равно нулю	Если же решается аннуитетная задача, в которой известен размер платежа, а дополнительные единовременные начальные вложения отсутствуют, то в силу условия PV=0 элиминируется первое слагаемое, и остается зависящая от размера платежа формула будущей стоимости аннуитета с начислением процентов за период между платежами.
Получается балансовая модель роста сложных процентов, учитывающая направление движения средств: то, что дали в долг – положительно, а то, что будет потом возвращаться кредитору с процентами обратно, с точки зрения должника, отрицательно	Второй сомножитель по умолчанию равен единице (случаю постнумерандо соответствует тип=0), а если оценивается аннуитет пренумерандо (тип=1), то получается процентный множитель (1+RATE), отражающий дополнительный период начисления сложных процентов за счет более раннего начала поступления потока платежей Для существования ненулевых корней этого соотношения знаки величин затрат и поступлений должны быть друг другу противоположны

Пример. Инвестор выдает должнику кредит в объеме 300 тыс. руб. Возврат долга планируется в виде квартального аннуитета с выплатой 75 тыс. руб. постнумерандо (обыкновенной финансовой ренты) на протяжении 5 кварталов.

Оценим процентную ставку R за один квартал. Подставляя исходные данные в формулу текущей стоимости аннуитета, получаем следующее уравнение относительно новой переменной x = (1 + R) – процентного множителя за один квартал:







Рис. 55. Поведение заданного многочлена шестой степени от ставки R на интервале [0%; 10%].

Глядя на график этой функции, построенный на рис. 55 в зависимости от значений квартального процента R, можно предположить, что искомый ответ находится в районе 7–8% и подобрать его итеративно. Выявив графически интервал значений ставки, внутри которого находится ответ, например, [6%;11%], необходимо проверить подстановкой в условия задачи какую-нибудь внутреннюю точку, и по результатам проверки сузить область поиска, сдвинувшись левее или правее. Так постепенно с заданной точностью подбирается процент аннуитета. Встроенная функция финансовая функция RATE=НОРМА работает не по аналитической формуле (в общем случае ее не существует!), а обращается к процедуре итеративного подбора корней многочлена методом Ньютона3.



Рис.56 Применение функции НОРМА=RATE для нахождения доходности аннуитета.

Задание Используя процедуру Excel Подбор параметра, подгоните к 300 тыс. руб. значение суммы строки нулевого периода в "верхнем аннуитетном треугольнике" (см. рис. 57). Какая процентная ставка R за период доставляет эту текущую стоимость? Повторите подбор, используя в качестве зависимой от исходного значения ставки R формулы обращение ко встроенной функции PV=ПЗ.

Рис. 57. "Верхний аннуитетный треугольник".

Задание Каким должен быть размер периодического платежа, чтобы внесение пяти одинаковых платежей такого размера по схеме постнумерандо позволило погасить долг 300 тыс. руб. по ставке 8% за период?

Проценты начисляются на невыплаченную часть долга ("правило США4"). При соблюдении равенства периодических платежей друг другу изменяется пропорция между двумя составными частями платежа (см. рис. 58).



Рис.58. Сравнение графиков погашения долга.

Сначала по аннуитетной формуле (здесь это сделано при помощи функции PMT=ППЛАТ) определяется сумма платежа – 75 137 тыс. руб. Затем каждый платеж разбивается на части следующим образом: PMT = PPMT + IPMT.



Меньшая и постоянно уменьшающаяся часть платежа IPMT (от англ. interest payment): 24000, 19909, 15491, 10719 и 5566 соответствует процентам на остаток долга, который постепенно погашается. Долг уменьшается каждый раз не на всю сумму платежа, а только на его растущую часть PPMT (от англ. principal payment), остающуюся после уплаты процентов за непогашенный долг предыдущего периода:

1 кв.: 8%*300000=24000, погашение 75137–24000=51137, остаток 300000–51137=248863

2 кв.: 8%*248863=19909, погашение 75137–19909=55228, остаток 248863–55228=193635

3 кв.: 8%*193635=15491, погашение 75137–15491=59646, остаток 193635–59646=133989

4 кв.: 8%*133989=10719, погашение 75137–10719=64418, остаток 133989–64418= 69571

5 кв.: 8%* 69571= 5566, погашение 75137– 5566=69571, остаток 69571–69571= 0.

Сумма всех частей платежа PPMT, погашающих долг, равна 300 тыс.руб. Дисконтированная же по ставке кредитования (процент в данном примере R = 8%) сумма платежей PMT также равна исходной сумме долга. Для расчета частей периодического платежа, размер которых зависит от текущего периода k, в Excel также имеются встроенные функции PPMT и IPMT (см. табл. 16).

Таблица 16

Функции для расчета частей платежа при погашении долга равными платежами

Показатель	Встроенная функция Excel
Погашение основного долга	ОСНПЛАТ(норма;период;кпер;тс;бс;тип)
Principal Payment	PPMT(rate;k;nper;pv;fv;type)
Процентная часть платежа	ПЛПРОЦ(норма;период;кпер;тс;бс;тип)
Interest Payment	IPMT(rate;k;nper;pv;fv;type)

Так, например, можно получить разбиение второго платежа на погашение основного долга –55,228=PPMT(0,08;2;5;300) и процентную часть –19,909=IPMT(0,08;2;5;300).

Можно предложить бесконечно много других способов разбиения во времени выплаты основного долга и процентов по нему на несколько частей. Одной из наиболее распространенных простых и стандартных схем, используемых в российской практике является равномерное погашение, при котором одинаковы не общие суммы платежей, а их только части, погашающие долг. Сумма нескольких равных частей, погашающих долг, равна исходной сумме долга. Тогда процентная часть считается по ставке за период умножением на равномерно убывающий долг, а размер каждого отдельного платежа выводится как сумма двух частей. Дисконтированная по ставке кредитования сумма платежей по-прежнему равна исходной сумме долга.





Рис.59. Эквивалентность потоков платежей погашения долга по разным схемам.

Обе рассмотренные схемы погашения долга: и равными платежами, и неравными, эквивалентны друг другу по начальной стоимости кредита. Это обстоятельство иногда используют в анализе инвестиционных проектов, вычисляя аннуитет (размер годового платежа), эквивалентный исходному денежному потоку в смысле равенства чистого дисконтированного дохода. При простом арифметическом суммировании всех платежей без дисконтирования эти потоки друг от друга отличаются, но с точки зрения экономической теории процента, такое "измерение дохода" за несколько периодов не имеет смысла, поскольку полагает цену денег во времени равной нулю, что на финансовом рынке невозможно.

Пример. Кредитование физических лиц на приобретение автомобилей5.

Сравним по данным рис. 60 два предложения о выдаче кредита на приобретение автомобиля ВАЗ-21213.



Рис. 60. Определение годовой процентной ставки платы за кредит по сумме долга, сроку и размеру ежемесячного платежа.



Рис. 61. Прямая зависимость между платой за кредит и суммой периодического платежа.

Задание Составьте план погашения долга 1750 долл. США 24 равными ежемесячными платежами по ставке 16% годовых. Используйте при выполнении задания встроенные финансовые функции Excel.

Альтернативный план равномерного погашения кредита с теми же параметрами представлен ниже в табл.17. Сумма частей платежа, погашающих долг, равна исходной сумме кредита.

Таблица 17

План погашения автомобильного кредита.

Месяц	Остаток долга	Погашение долга	Проценты	Платеж
0	1750,00
1	1677,08	72,92	22,36	95,28
2	1604,17	72,92	21,39	94,31
3	1531,25	72,92	20,42	93,33
4	1458,33	72,92	19,44	92,36
5	1385,42	72,92	18,47	91,39
6	1312,50	72,92	17,50	90,42
7	1239,58	72,92	16,53	89,44
8	1166,67	72,92	15,56	88,47
9	1093,75	72,92	14,58	87,50
10	1020,83	72,92	13,61	86,53
11	947,92	72,92	12,64	85,56
12	875,00	72,92	11,67	84,58
13	802,08	72,92	10,69	83,61
14	729,17	72,92	9,72	82,64
15	656,25	72,92	8,75	81,67
16	583,33	72,92	7,78	80,69
17	510,42	72,92	6,81	79,72
18	437,50	72,92	5,83	78,75
19	364,58	72,92	4,86	77,78
20	291,67	72,92	3,89	76,81
21	218,75	72,92	2,92	75,83
22	145,83	72,92	1,94	74,86
23	72,92	72,92	0,97	73,89
24	0,00	72,92	0,00	72,92

<


1 платеж: проценты 16%/12*1750=22,36 погашение 1750/24=72,92 всего 72,92+22,36=95,28

2 платеж: остаток долга1750-22,63=1677,08 проценты 16%/12*16677,08=21,39 и т.д.

Задания

Используя данные табл. 18, сравните предложения конкурирующих банков о предоставлении кредита на покупку автомобиля ГАЗ –3110 по уровню годовой доходности.

Используя прогноз параметров динамики курса рубля, используемый в государственном бюджете РФ, попробуйте составить план погашения кредита в сумме 2000 долл. США 24 ежемесячными платежами, для случая, когда валютой кредита являются рубли по ставке 32% годовых.

Таблица 18

Условия кредитования на приобретение автомобилей.

Марка-модель	Цена, долл.США	Срок кредита, месяцев	Единовр. взнос, долл.США	Сумма кредита, долл.США	Ежемесячный платеж, долл.США
ГАЗ — 3110	4000	24	2000	2000	96.97
ГАЗ — 3110	4000	24	2000	2000	98.88
ГАЗ — 3110	4000	24	1200	2800	139.79
ГАЗ — 3110	4000	30	1200	2800	113.85

Задание Используя процентные ставки табл.19, составьте и сравните между собой таблицы ежемесячного погашения кредитов в сумме 2800 долл. США на разные сроки как в иностранной валюте, так в и рублях. Какой темп роста курса доллара приводит к безразличию выбора валюты договора?

Таблица 19

Годовая доходность кредитов физическим лицам на приобретение автомобилей

Валюта кредита	Ставка, % годовых
	на срок до 180 дней	на срок от 181 дня до 1 года	На срок от 1 года до 2 лет
Рубли РФ	27	29	32
Доллары США	13	15	17

Задание Покупатель ВАЗ2110 не может заплатить единовременно предложенную дилером цену 5000 долл. и выбирает наиболее привлекательные условия для приобретения автомобиля в кредит. Какую альтернативу Вы бы предпочли? Аванс 2500 долл. плюс 24 платежа по 150 долл. Кредит выдается в долларах США. Аванс 1560 долл. плюс 24 платежа по 5250 рублей. Валюта кредита – рубли РФ. В конце срока кредита машина продается, и ее цена (не ниже 1300 долл.) зачитывается в счет покупки новой машины.

3 См., напр.: Уотшем Т. Дж., Паррамоук. Количественные методы в финансах. М., 1999.

4 См., например, статью «United States rule» в Федоров Б.Г. «Англо-русский толковый словарь валютно-кредитных терминов». – М., 1992.

5 По материалам специализированного автокредитного сайта http://www.carloan.ru

Современные учебники финансового менеджмента все

Современные учебники финансового менеджмента все чаще прямо адресуются к Excel как средству выполнения расчетов. Электронные таблицы исторически и были задуманы как программное средство решения пользователем ПЭВМ задач финансового учета и анализа. Справочные издания с корректным изложением теоретического материала, лежащего в основе аппарата встроенных финансовых функций появляется и на русском языке1. Предпринимаются попытки перевода работ зарубежных специалистов, имеющих большой практический опыт успешного решения учетных задач электронными таблицами2.
Вместе с тем, при самостоятельном освоении программы необходимо иметь в виду, что изложение теоретических основ и методических принципов работы некоторых встроенных процедур Excel, например математического программирования, многомерного статистического анализа и управления списком записей как однотабличной базой данных, является предметом специальных учебных курсов, входящих в программу университетской подготовки экономиста. Полное руководство по Excel занимает тысячу страниц3, но даже при этом в учебных целых многие темы должны быть дополнительно поддержаны методическими разработками преподавателя высшей школы.
Учебный материал данного пособия может использоваться самостоятельно или служить вводной частью для курсов "Финансовый менеджмент" и "Управленческий учет" для студентов, уже знакомых с основами дисциплины "Экономическая информатика".
Литература
Башарин Г.П. Начала финансовой математики. М.: ИНФРА-М, 1998.
Ковалев В.В., Уланов В.А. Курс финансовых вычислений. М.: Финансы и статистика, 2001. Уланов В.А. Сборник задач по курсу финансовых вычислений. М.: Финансы и статистика, 2001.
Капитоненко В.В. Финансовая математика и ее приложения. М.: Приор, 2000.
Кутуков В.Б. Основы финансовой и страховой математики: Методы расчета кредитных, инвестиционных, пенсионных и страховых схем. М.: Дело, 1998.
Малыхин В.И. Финансовая математика. М.: Юнити-Дана, 1999.
Мелкумов Я.С. Теоретическое и практическое пособие по финансовым вычислениям. М.: Инфра-М, 1996.
Салин В.Н., Ситникова О.Ю. Техника финансово-экономических расчетов. М.: Финансы и статистика, 1998.
Четыркин Е.М. Финансовая математика. М.: Дело, 2001.

1 Овчаренко Е.К., Ильина О.П., Балыбердин Е.В. Финансово-экономические расчеты в Excel. М., 1999; Лукасевич И.Я. Анализ операций с ценными бумагами с Microsoft Excel. - http://www.cfin.ru/finanalysis/inexcel

2 Карлберг К. Бизнес-анализ с помощью Excel 2000. Киев., 2000.

3 Додж М., Кината К., Стинсон К. Эффективная работа с Microsoft Excel 97. СПб, 2000.
 

---

---